My research activities range from biomechanics and fluid dynamics to applied mathematics. My research areas are mainly focused on direct numerical simulations of complex fluids. Here is a brief description of my areas of expertise. Please contact me (afkhamis@math.vt.edu) or see my publications for more details.

Modelling Incompressible Two-Phase Flows:

Two-phase flows appear in many natural and practical processes. Applications range from environmental sciences to nuclear industries. Spreading behaviour of pesticide droplets, interfacial instabilities at the atmosphere-ocean interface, spray cooling, and the formation of droplets in combustion chambers are but a few examples in which the study of liquid-gas interfaces is important. These phenomena often occur on very small time and space scales. In such cases, experimental visualization is difficult and very complex. Therefore, numerical simulations are, in practice, necessary to investigate these flows. However, a numerical method for modelling two-phase flows can be very difficult to implement since it depends on characteristics of the physical phenomena that are complex to model. These include the shape of the interface, the dramatic density ratio between gas and liquid, and the presence of surface tension that is a function of the topology of the interface.

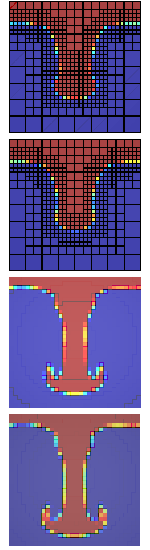
Adaptive mesh refinement

Adaptive mesh refinement methods have recently been a focus of much research. In general, numerical technique accuracy depends on the spatial resolution of the applied discretisation. But making the mesh finer and finer increases runtime, and simulation size will always be limited by the available computing resources. On the other hand, because of the nature of some problems, the finest resolution is often required only in a small fraction of the flow domain. One such example is droplet impact. When simulating the flow within and around an impacting droplet, high resolution is required in the small region beneath the droplet at the moment of impact, while in the rest of the domain, the solution is of less interest. Later in the simulation, high resolution will be concentrated on small-scale features like fingers and satellite droplets.

Formulation of the problem

The governing equations describing the motion of an incompressible two-phase flow are the Navier-Stokes equations. Density and viscosity are considered to vary from phase to phase but are assumed constant in each phase. These equations are a "one-fluid" continuum formulation over the whole domain, and therefore, a separate methodology must be used to identify the interface topology. A "PLIC" algorithm is utilized for following the deformation of the interface.

Cell-centered variable-density projection method

The discretisation is based on the variable-density fractional-step scheme utilizing collocated positioning. Each time-step consists of four parts: 1) Using a second-order upwind scheme and the "MAC" projection method to calculate velocities on cell faces at the half time-step.
2) Advecting the volume fractions. 3) Reconstructing the density and viscosity using the new information computed in step (2). 4) Using an approximate projection method to calculate the cell-centered velocities at the next time-step.

Numerical simulation
Screenshots of the spreading behaviour of a water droplet impacting with a velocity of 0.5 m/sec onto a solid surface are pictured. The radius of the droplet is 0.2 mm, the surface tension coefficient is 0.073 N/m, and the density ratio is 820:1. The contact angle is set to be 105 degrees.

Download
CCAP-VOF 0.2.0 (interested? e-mail me)

References
1- A. M. Khokhlov:  Fully threaded tree algorithm for adaptive refinement fluid dynamics simulations , J. Comput. Phys., 143, 519-543, 1998.
2- S. Popinet:  Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries , J. Comput. Phys., 190,
    572-600, 2003.
3- D. Gueyffier et al.:  Volume-of-fluid interface tracking with smoothed surface stress methods for threedimensional flows , J. Comput.
    Phys., 152, 423-456,
4- S.Popinet:   The Gerris Flow Solver , http://gfs.sourceforge.net.

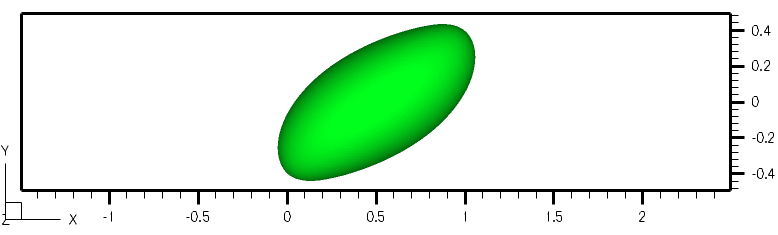
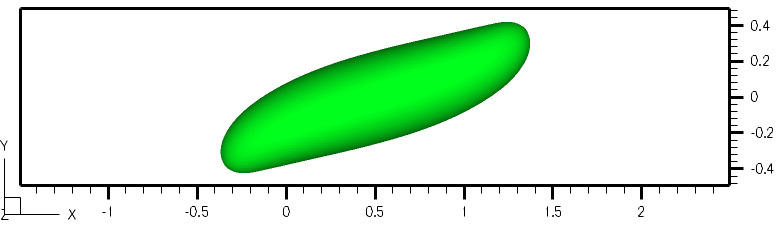
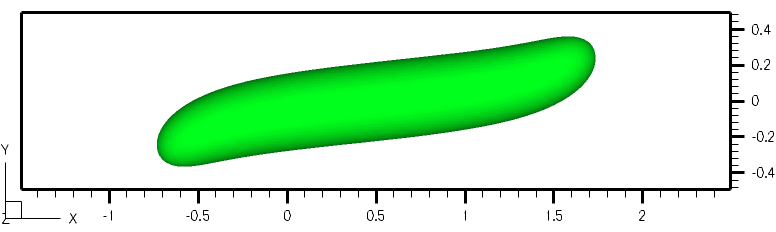
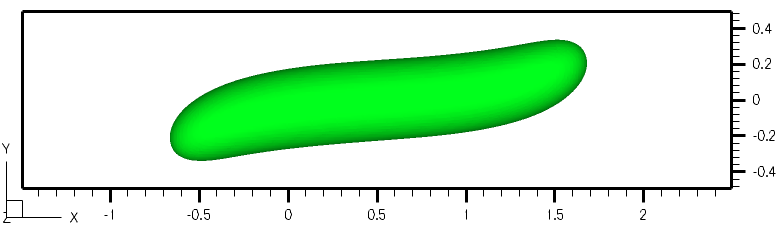
Numerical Simulation of Ferro-droplets:

Ferrofluids consist of magnetic nanoparticles in a colloidal solution. Recent developments in the synthesis and characterization of ferrofluids are motivated by biomedical applications. In magnetic drug targeting, for example, the understanding of the interaction of an external magnetic field with blood flow containing ferro-droplets is of significant interest. The governing equations are the Maxwell equations for non-conducting flows and Navier-Stokes equations for immiscible and incompressible two-fluid systems. We numerically study the interfacial dynamics of ferro-droplets in non-magnetic viscous media subjected to magnetic field gradients. Influenced by the presence of a non-uniform magnetic field, ferrofluid droplets deform to prolate droplets in the direction of the magnetic field. The figure shows that the droplet undergoes deformation due to the presence of an external magnetic field gradient. The droplet magnetic Bond number is 0.05.

Breakup of Viscoelastic Drops:

At high capillary numbers such as Ca=0.5, a Newtonian drop in a viscoelastic matrix under shear breaks up. Here, we show 3D breakup process for viscosity ratio 1 and at Ca=0.5 and De=0.75. Viscoelastic stresses are built up at the interface outside the tip of the drop, pulling the ends out. Numerical simulations are shown with contour plots of the trace of the extra stress tensor in the velocity-velocity gradient plane at non-dimensional times 87.5 and 91.2.

Electrowetting on Dielectric (EWOD):

Electrowetting is a technique that utilizes an applied electric field to change the wetting behaviour of a fluid on a solid surface. By applying a spatially-varying field, the wetting behavior will change spatially, and cause a drop of fluid to move on the surface. There have been recent attempts to simulate such forced movement of a droplet on a surface, a problem also of interest in microfluidic processing. Here, we present the results of a simulation that illustrates such a behavior, by prescribing a spatially-varying contact angle. A hemispherical droplet of radius R=200 micrometers is initially placed at the bottom of a 1mm x 1mm x 1mm domain; the fluid properties are those of water and air. The droplet is at rest (contact angle is 90 degrees) when suddenly a 60 degree and 120 degree contact angles are imposed beneath halves of the droplet. A sequence of results are shown and illustrate how the droplet is quickly drawn from the non-wetting to the wetting surface, which leads to transient contact line profiles that are far from axisymmetric. Results are shown at 0, 2, 5, 7, 12, and 30 msec from top to bottom.

Volume-of-Fluid Based Approach for Simulating Moving Contact Lines:

Here we show results of the impact of a droplet on an inclined surface. The figure illustrates numerical simulations of the oblique impact of a droplet onto a 45 degree incline for Re = 300 and We = 250. Simulations are run on adaptive meshes. For these simulations, the calculated variation of receding contact angle = 45 and advancing contact angle = 135 are imposed about the contact line. Advancing or receding contact angles vary linearly with contact line velocity and approach asymptotic values as the contact line velocity increases.

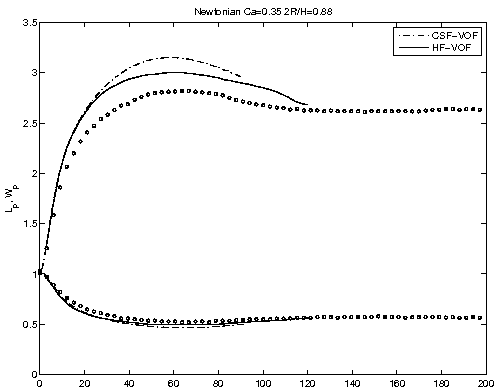
Microconfined Fluid Droplet in Shear Flow:

The behavior of a microconfined Newtonian droplet in a Newtonian matrix is studied. The viscosity ratio is 1, 2R/H is 0.88, and Ca is 0.35. The dimensionless drop length L and width W are observed from above and are given for the experimental data (o) vs our numerical results (---). The figure shows drop shapes from the side at non-dimensional times 3, 9, 30, 120. Our results compare well with the experimental data.

Numerical Modelling of Sliding Droplets:

A numerical dynamic contact angle model based on a well-known hydrodynamic theory is developed for the imposition of a boundary condition at the contact line. The efficacy of this new model is demonstrated via 3D examples of a viscous droplet sliding down a partially wetting incline. As experimentally observed, when the inclination angle increases, the rear of the drop becomes elongated until it develops a ''corner'' which eventually breaks up into smaller droplets, while the leading edge of the drop remains rounded. Here, we present the results of droplets sliding on an inclined plane. A similar behaviour (asymmetry between advancing and receding contact lines) is demonstrated. Results are in qualitative agreement with experimental observations. The role of surface inclination on the distribution of the dynamic contact angle along the droplet perimeter is also presented.