|
Independent or Not Independent| Exercise 1.6-2 | Example 1.6-6 | Useful Web Resources| Solutions
Sample Spaces and Events
Defintion 1.6-1
The events A and B are independent if P(A ∩ B)= P(A)P(B)
Theorem 1.6-1

Example 1:
Consider rolling a dice twice. Let A be the event of rolling a 5 on the first roll, and let B be the event of rolling a 3 on the second roll.
P( 3 | 5)=P(3)= 1/6 because each roll of the dice is independent of one another. That is, the outcome of the first roll does not affect the outcome of the second roll. So the probability of rolling a 3 on the second roll is 1/6
P( 5 | 3)=P(5)= 1/6 because whether we observe B or not, the probability of rolling a 5 on the first roll is 1/6
P(5 ∩ 3)= P(5)P(3)= (1/6)x(1/6) because the outcome of the first roll does not affect the outcome of the second roll.
Note: Mutually exclusive events and the notion of independent events should not be confused with one another. If two events with nonzero probability are mutually exclusive, then by defintion P(A ∩ B)=0, but P(A)P(B) >0. Then condition iii of in theorem 1.6-1 does not hold. The events are not independent. Therefore mutually exclusive events cannot be independent events.

Independent or Not Independent?
Using the conditions given in Theorem 1.6-1, identify the Independent events.
A: Consider drawing 2 cards, one after another, without replacement, from a deck of cards. A is the event of drawing a 7 on the first draw, and B is the event of drawing a 6 on the second draw.
B: Consider rolling a dice twice. A is the event of rolling a 4 on the first roll, and B is the event of rolling an even number on the second roll.
C: A is the event that gas prices are high today. B is the event that gas prices are high tommrow.
Solution

Exercise 1.6-2:
In a particular board game a player rolls a pair of fair dice on each turn. In order to move a game piece the player must roll a 5 on at least one of the die or a sum of 5 on the two dice. Let A be the event "a 5 on at least one die", and let B be the event "the sum of the face values is 5."
A: What is P(A)?
|
B: What is P(B)?
|
C: What is P(A ∩ B)?
|
D: Are A and B independent?
|
Solution

Example 1.6-6:

Intuitively, events are mutually independent if the act of observing any set of them has no effect on the probabilities of occurrence of any other events.
Consider the following system that contains 6 components. The system will work if components 1,2,3,4 all work or if 5 and 6 both work. Assume the components are mutually independent and components 1,3, and 5 have a probability of 0.6 of working, and the rest of the components have a probability of 0.75 of working.
Let Wi denote the event "component i works". In set notation, this event is (W1 ∩ W2 ∩ W3 and ∩ W4 ) (W5 ∩W6). (W5 ∩W6).
Refer to Example 1.6-7 of your text, and answer the following questions.
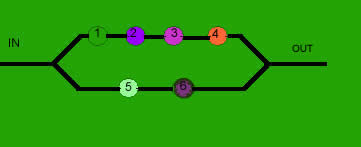
Round your answers to 3 decimal places.
Solution

Useful Web Resources
Lesson on Probability
GoMath Mini Lessons
Statistics Glossary

A: A and B are NOT independent because after drawing a 7 in the first draw, there are 51 cards left in the deck. So the outcome of the first draw does affect the outcome of the second draw.
B: A and B are independent events because the outcome of the first draw does not affect the outcome of the second draw.
C: A and B and NOT independent events because if the gas prices are high today, the gas prices tommrow are likely to be high as well.

A= {(1,5) , (2,5), (3,5), (4,5) (5,5), (6,5)} because the dice are identical, so the order does not matter.
B={(2,3), (4,1)}
S= { (1,1) , (1,2), (1,3), (1,4) (1,5), (1,6), (2,2),(2,3), (2,4),(2,5), (2,6), (3,3), (3,4) (3,5) (3,6) (4,4) (4,5) (4,6) (5,5), (5,6) , (6,6)}
So P(A)=6/21=0.29, and P(B) =2/21=0.095=0.10 and P(A ∩ B)=0 but P(A)P(B)=0.029>0. So condition iii in theorem 1.6-2 does not hold. Therefore the events are not independent.

Components 1, 3 and 5 have a probability of 0.6 of working. So P(1)=P(3)=P(5)= 0.6. Compenents 2,4, and 6 have a probability of 0.75 of working. So P(2)=P(4)=P(6)=0.75
A: P(W1 ∩ W2 ∩ W3 ∩ W4)= P(1)P(2)P(3)P(4)= (0.6)(0.75)(0.6)(0.75)=0.2025=0.203
B: P(W5 ∩ W6)= P(5)P(6)=(0.6)(0.75)=0.450
C: P(W1 ∩ W2 ∩ W3 ∩ W4 ∩ W5 ∩ W6)= P(1)P(2)P(3)P(4)P(5)P(6)= (0.6)(0.75)(0.6)(0.75)(0.6)(0.75)=0.091
D: The probability that the system will work is P(W1 ∩ W2 ∩ W3 ∩ W4)+P(W5 ∩ W6) - P(W1 ∩ W2 ∩ W3 ∩ W4 ∩ W5 ∩ W6). We must subtract the probability of all the components working.
So P(W1 ∩ W2 ∩ W3 ∩ W4) + P(W5 ∩ W6) - P(W1 ∩ W2 ∩ W3 ∩ W4 ∩ W5 ∩ W6). = 0.203 + 0.45 -0.091 = 0.562

|