|
Example 1| Example 2 | Useful Web Resources| Solutions
Definition 2.2-1:
The joint probability mass function of the discrete random variables X and Y is a function p(x,y) defined by
p(x,y) = P( X=x, Y=y)
where (X= x, Y= y) denotes the intersection of the events (X= x) and (Y= y).
Example 1:
Consider an experiment that studies the number of people with colourblindness in a group of 300 people. Let X represent the gender of the subject (0= Male, 1=Female), and let Y represent whether or not someone is colourblind (0=Not Colourblind, 1= Colourblind). The joint probability mass function of X and Y is given below:
| p(x,y) |
Male=0 |
Female=1 |
| Not Colourblind=0 |
112/300 |
140/300 |
| Colourblind=1 |
33/300 |
15/300 |
*Referenced from http://www-stat.stanford.edu/~susan/courses/s116/node65.html
So p(0,1)=112/300 is the probability that a randomly selected male is not colourblind.
From the joint probability distribution the distributions of X and Y can be found. The probability of being colourblind can be found by summing all entries in the table for which Y=1.
So P(Y=1) = 33/300+15/300 = 48/300
Round all answers to 2 decimal places.
Solution

To find probablities such as P(X=0) and P(Y=0) we added the entries in the table over a row or a column to obtain the marginal total. In the context of joint probability distributions, the probability mass functions of the individual random variables are called marginal probability mass functions.
Definition 2.2-2: Marginal Probability Mass Functions
Let X and Y be discrete random variables with joint probability distribution P(X=x, Y= y). The marginal probability mass functions of X and Y are
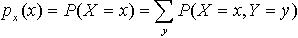
and

The marginal mass functions for X and Y in Example 1 are added to the table:
p(x,y) |
Male=0 |
Female=1 |
Py(Y) |
Not Colourblind=0 |
112/300 |
140/300 |
252/300 |
Colourblind=1 |
33/300 |
15/300 |
48/300 |
Px(X) |
145/300 |
155/300 |
1 |

Definition 2.2-3: Conditional Probability Mass Function
The conditional probability mass function of Y given X= x is defined for all x such that px(x)>0 as

Example 2:
Refer to Example 2.2-2 on page 53. Answer the follwing questions.
Round all answers to 2 decimal places.
Solution

Definition 2.2-4:
The discrete random variables X and Y are independent if, for all values of x and y,
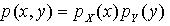
Otherwise the random variables X and Y are dependent.
Example 3:
Refer back to Example 2.2-2 on page 53. Are X and Y independent?
Solution:
p(3,3)=1/16. P(X=3)=1/2 and P(Y=3)=5/32. Therefore p(3,3) does not equal p(X=3,Y=3). So X and Y are dependent.
Definition 2.2-5


Useful Web Resources
Joint, marginal, and Conditional Distributions-Statistical Engineering
Joint Distributions
Joint Distributions- Wikipedia
Conditional Distributions- Wikipedia
Discrete Conditional Distributions- www.math.mcmaster.ca/canty/ teaching/stat2d03/lectures9.pdf

Solutions
Solution to Example 1
A: To find the probability of being a male, you have to add up the values in the column pertaining to X=0. So we get 112/300 +33/300=145/300=0.48
B: To find the probability of being a female, you have to add up the values in the column pertaining to X=1. So we get 140/300+15/300=155/300=0.5166=0.52
C: To find the probability of not being colourblind, you have to add across the values in the row pertaining to Y=1. So we get 112/300 + 140/300 =252/300=0.84
D: P(Y=1|X=1) is interpreted as the probability that someone is colourblind given that they are a female. We know that P(Y=1|X=1)= P(Y=1,X=1)/P(X=1) =(15/300) /(155/300) =15/155=0.096=0.10

Solution to Example 2
A: P(X+Y)= P(2,2)+ P(3,1)+P(1,3)=3/16 +1/16+1/32=9/32=0.28125=0.28
B: P(Y<3) =P(2,1)+P(2,2)+P(2,3)+P(2,4)+P(1,1)+P(1,2)+P(1,3)+P(1,4)
= Py(1)+Py(2)=5/32+11/16=27/32=0.84375=0.84
C: P(X>=2)=Px(2)+Px(3)+Px(4)=1/4+1/2+1/8=7/8=0.875=0.88
D: P(Y>=2 |X=2)=P(2,2)+P(2,3)=3/16+1/32=7/32=0.21875=0.22

.
.
|