Variance and Standard Deviation

Example 1| Example 2 | Example 3 | Useful Web Resources| Solutions

Definition 2.4-1: Variance and Standard Deviation

For a random variable X, the variance of X, VAR(X), and the standard deviation of X, STD(X), are defined as:

• The standard deviation of a random variable is in the same units of measurement as the random variable
• The variance is in the square of the original units

Example 1:

Suppose the random variable X has the following probability distribution:

x	-1	0	1	2	3	4
p(x)	0.05	0.20	0.30	0.30	0.10	0.05

 

What is VAR(X)?



= (-1-1.35)^2 (0.05) + (0-1.35)^2(0.2) + (1-1.35)^2(0.3)

+ (2-1.35)^2(0.3) + (3-1.35)^2(0.1) + (4-1.35)^2(0.05) =

(Round to 4 decimal places)

 

What is STD(X)?

(Round to 4 decimal places)

Solution

 

*Explore mean and standard deviation using this applet!

Theorem 2.4-1: Chebychev's Inequality

Let X be a random variable with E(X)= u and STD(X) =s . For any k>0,

• Chebychev's inequality states that the probability a random variable falls within +/- k standard deviations of its expected value is at least 1-(1/k^2).
• For example , at least 1-(1/2^2)=0.75, or 75% of the time, a random variable will fall within +/- 2 standard deviations of its mean.
• Similarly, 1-(1/3^2)=0.89, or 89% of the time, a random variable will fall within +/- 3 standard deviations of its mean.

Theorem 2.4-2:

• If Y = a + bX, where a and b are constants, then

  

  and

  

   

Example 2:

Consider the random variable X, that has the following probability distribution.

x	-2	-1	1	2	4
p(y)	0.20	0.40	0.10	0.10	0.20

 

Let Y=97-6X. Complete the table below. Please round all your answers to 2 decimal places.

What is E(X)?	What is VAR(X)?
What is STD(X) ?	What is E(Y)?
What is VAR(Y)?	What is STD(Y)?

Solution

Theorem 2.4-3:

 

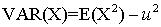
Example 3:

Consider the random variable X from Example 1.

E(X^2)= (-1)^2(0.05)+ 1^2(0.3) + 2^2(0.3) +

3^2(0.10) + 3^2(0.10) + 4^2(0.05)=

(Round to 2 decimal places)

 

Calculate the VAR(X) in Example 1 using theroem 2.4-3.

(Round to 2 decimal places)

 

Solution

---

Useful Web Resources

Variance and Standard Deviation- Statistics Canada

Math Centre:Variance and Standard Deviation- http://mlsc.lboro.ac.uk/documents/var_stand_deviat_ungroup.pdf

Mean, Standard Deviation and Variance applet

Chebychev's Theorem

---

 

Solutions

 

Solution to Example 1

Var(X)= (-1-1.35)^2 (0.05) + (0-1.35)^2(0.2) + (1-1.35)^2(0.3)+ (2-1.35)^2(0.3) + (3-1.35)^2(0.1) + (4-1.35)^2(0.05)

=0.276125 + 0.3645+0.03675+0.12675+0.27225+0.351125=1.4275

STD(X)=sqrt(VAR(X))=1.194780315=1.19748

Solution to Example 2

x	-2	-1	1	2	4
p(y)	0.20	0.40	0.10	0.10	0.20

E(X)= -2(02)-1(0.4)+ 1(0.1)+2(0.1)+4(0.2) =0.3

VAR(X)= (-2-0.3)^2(0.2) + (-1-0.3)^2(0.4) + (1-0.3)^2(0.1) + (2-0.3)^2(0.1) + (4-0.4)^2(0.2)

=0.072345567 + 0.676 + 0.049 + 0.289 + 2.738

=3.143345567

=3.14

STD(X)=sqrt(3.14)=1.77

VAR(Y)=VAR(97-6X)= 0+36VAR(X)=36(3.14)=113.04. (Remember -6 gets squared to give you +36.

VAR(97)=0 because the variance any constant is 0)

STD(Y)=sqrt(113.04)=10.63

Solution to Example 3

E(X^2)= (-1)^2(0.05)+ 1^2(0.3) + 2^2(0.3) + 3^2(0.10) + 3^2(0.10) + 4^2(0.05)

= 0.05+0.3+1.2+0.9+0.8

=3.25

..

 

.

Created by Ranodya Upathilake © Copyright 2002-2003. All rights reserved. Free Web Site Templates by JimWorld.com Designed by Finerdesign.com | Comments or Questions?