Sta107 Online Tutorial

Definition 3.5-1:

The poisson probability mass function is defined on the non-negative integers and has functional form

Theorem 3.5-1:

Let X denote a Poisson random variable with probability mass function given in Definition 3.5-1. Then,

E(X) = u and VAR(X)= u

Theorem 3.5-2:

Let X be a binomial random variable based on a sequence of n independent and identical Bernoulli trails with proabability p of success on each trail. If n --> ¥ and p--> ¥ in such a way that the mean u = np is constant, then

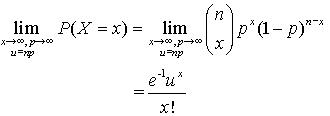
Example 1:

Customer arrivals at a service station following a Poisson process with rate u= 5 customers per hour.

What is the probability that 2 customers arrive in the next hour?

Solution:

u=5 and x=2. So p(2)= [e^(-5)] (5^2)/(2!) = 0.0842

A: What is the probability that no customers arrive in the next hour?

(Round to 4 decimal places)

Solution

What is the probability that 2 or more customers arrive in the next hour?

Solution:

P(X>=2)= 1- P(X£1)

=1- [P(0)+P(1)]

= 1-[e^(-5)] (5^0)/(0!) + e^(-5)] (5^1)/(1!)]

=1-[ 0.0067+0.0337]

=1-0.0404

=0.9596

B: What is the probability that 3 or more customers arrive in the next hour?

(Round to 4 decimal places)

Solution

Example 2:

The probability of hitting the bullseye in a dart game is 0.2. Since each throw of the dart is independent of one another, then the number of bullseyes in 50 throws has a binomial distribution with n=50 and p=0.2. We use a Poisson approximation to the binomial with u=np=50(0.2)=10. If X deontes the number of bullseyes then what is P(X>3)?

Solution:

P(X>3)=1-P(X£3)

= 1- [P(0)+P(1)+P(2)+P(3)]

=1- [e^(-10) (10^0) / (0!) + e^(-10) (10^1)/ (1!) + e^(-10) (10^2) / (2!) + e^(-10) (10^2) / (2!) ]

=1-0.0103

=0.9897

What is P(X>=6)? (Use table 3 in the Appendix)

Example 3:

Refer to Exercise 3.5-2 on page 128. The number of jobs submitted per minute to a supercomputer center is a Poisson random variable with u=3.

Round all answers to 4 decimal places

A: What is the probability that there are 0 jobs submitted in any one minute?

B:What is the probability that there will be fewer than 2 jobs submitted in a minute?

C: What is the probability that there are more than 8 jobs submitted in a minute?

Solution

Explore the Poisson Distribution by using the following applet! Enter the value of u for Lambda.

Useful Web Resources

Solution to Example 1

A: u=5 and x=0. So p(0)= [e^(-5)](5^0) / 0!=0.006738=0.0067

B: P(X>=3) = 1- P(X£2)

=1- [P(0)+P(1)+ P(2)]

= 1-[e^(-5)] (5^0)/(0!) + e^(-5)] (5^1)/(1!) + e^(-5)] (5^2)/(2!)]

=1-[ 0.0067+0.0337+0.0842]

=1-0.1247

=0.8753

Solution to Example 2

P(X>=10)=1-P(X£9)

= 1- [P(0)+P(1)+...+P(9)]

=1-0.4579

=0.5421

Solution to Example 3

A: u=3 and x=0. So p(0)= [e^(-3)](3^0) / 0!= 0.0498

B: P(X<2)= P(X£1) =P(0)+P(1)= 0.1991

C: P(X>=8)=1-P(X£ 7)= 1-0.9881= 0.0119

.

.

Poisson Random Variables

Useful Web Resources

Solutions