.
The kth moment of a random variable X is defined to be E(X^k)
The first moment is the mean of X. The relationship between the second moment and variance is that

For a discrete random variable X with probability mass function p(x), the kth moment may be computed as
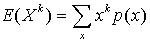
.
Example 1:
Let the random variable X have the following probability mass function.
x |
-1 |
0 |
1 |
2 |
p(x) |
0.3 |
0.2 |
0.1 |
0.4 |
.
What is the 4th moment of X?
Solution:
E(X^4)= (-1)^4(0.3) + (0)^4(0.2) + (1)^4(0.1) + ( 2)^4(0.4) = 0.3+ 0 + 0.1 + 6.4= 6.8
.
What is the 3rd moment of X?
.
For any positive integer k, the kth derivative of the moment-generating function with respect to t, evaluated at t =0, is the kth moment of the random variable X. The verification of this theorem for a discrete random variable X is as follows:
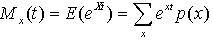

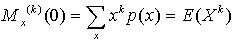
The mean and variance of a random variable X may be expressed in terms of the moment-generating function as
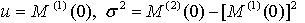

Example 2:
Let X have the following proability mass function:
.
What is the moment-generating function of X?
Solution:
Mx(t)= E(e^tx) = (e^0t)(0.5) + (e^1t)(0.1) + (e^2t)(0.4) =0.5+ 0.1(e^t) + 0.4(e^2t)
.
What are the first two moments of X?
Solution:
First moment
[Mx^(1)] (t) =0.1e^t + (0.4)(2)e^2t
= 0.1e^t + 0.8e^2t
Mean
u = [Mx^(1)] (0)= 0.1e^0 + 0.8e^(2*0)
=0.1+0.8
=0.9
Second moment
[Mx^(2)] (t) =0.1e^t + (0.8)(2)e^2t
= 0.1e^t + 1.6e^2t
Variance
[Mx^(2)] (0)= 0.1e^0 + 1.6e^(2*0)
=0.1+1.6
=1.7
So s^2=[Mx^(2)] (0) -{[Mx^(1)] (0)}^2 =1.7- 0.9^2 = 0.89

Example 3:
Let X have the following proability mass function:
x |
-1 |
0 |
2 |
p(x) |
0.2 |
0.7 |
0.1 |
Find the moment generatin function of X and use it to answer the following questions:
.
Solution
