If X is a continuous random variable with probability density function f(x), then the expected value is
Let X have the continuous probability density function defined by
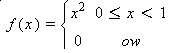
The expected value, variance and standard deviation are computed in the following way:
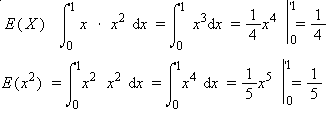
VAR(X) = E(X^2)- E(X)^2 = 1/5 - (1/4)^2 = 0.1375
STD(X) = sqrt(0.1375)= 0.37

Example 2:
Let the random variable X have the probability density function defined in Exercise 5.1-4 on page 200.
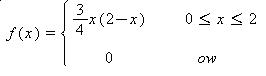
Solution

The mean and variance of a uniform [c,d] random variable are as follows:
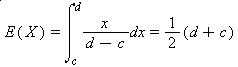
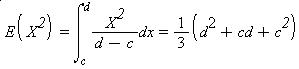
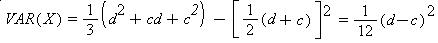

Example 3:
Let a random variable X have a uniform distribution.
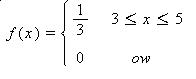
Solution
If Y= f(X) is an increasing or decreasing function, the probability density function can be written directly without the use of probability arguments. The function f(X) is increasing if for x1 £ x2, f(x1) £ f(x2) and it is decreasing if for x2£ x1, f(x2) £ f(x1).
Suppose Y= f(X) is an increasing function, then
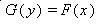
and
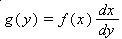
where x is expressed in terms of y by solving y = f(X) for x.
Suppose Y= f(X) is a decreasing function, then
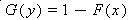
and
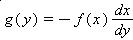

Example 4:
Consider the probability density function defined in Example 5.2-1 on page 204.
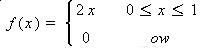
Let Y= X-1. Find G(y) and g(y).
Solution:
Step 1: Isolate X.
y = x-1
--> x = y +1
Step 2: Find the upper and lower bounds for y in terms of x.
0 £ X £ 1
0 £ y+1 £ 1
-1£ y £ 0
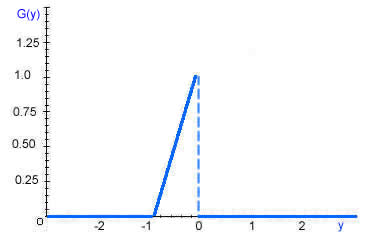
So y is defined between -1 and 0.
Step 3: Find F(X)
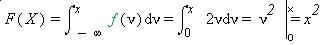
So x is defined between 0 and 1.
Step 4: Find G(y).
From step 1 we know that x= y+1 , and from step 3 we know that F(X) = x^2.
G(y) =F(x)
= F(y+1)
= (y+1)^2 where -1£ y £ 0
Step 5: Find g(y).
Since Y= x-1 is an increasing function, we find g(y) by using the equation
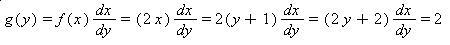
So g(y)=2 for -1£ y £ 0


Example 5
Refer to Exercise 5.2-11 on page 210. The probability density function for X is
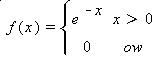
Let Y=X^2.
Solution
Free JavaScripts provided by The JavaScript Source

E(a+bX) = a +bE(X) and STD(a+bX)= |b|STD(X) for a continuous random variable X.

Useful Web Resources
Mean, Median, Variance and Standard Deviation
Uniform Distribution
Uniform distribution (continuous)- Wikipedia

Solutions
Solution to Example 2
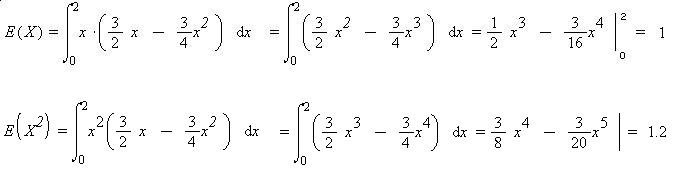
VAR(X)= 1.2- (1^2)= 0.2
STD(X)=sqrt(0.2)=0.447=0.45

Solution to Example 3
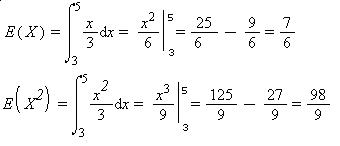
VAR(X)= 98/9 -(16/6)^2= 3.777=3.8
STD(X)= sqrt(3.8)=1.9

Solution to Example 5
Step 1: Isolate X.
y = x^2
--> x = sqrt(y)
Step 2: Find the bounds for y in terms of x.
X > 0
sqrt(y) >0
y > 0
Step 3: Find F(X)
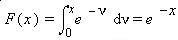
Step 4: Find G(y).
From step 1 we know that x = sqrt(y), and from step 3 we know that F(X) = exp(-x)
G(y) =F(x)
= F[sqrt(y)]
= exp(-sqrt(y)) where y >0
Step 5: Find g(y).
Since Y= X^2 is an increasing function, we find g(y) by using the equation
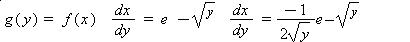
where y > 0.
