The mean, variance, and standard deviation of an exponential random variable X are
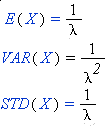
The cumulative distribution function is
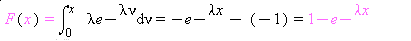

Example 1:
Assume that the amount of time it takes to complete a customer's transaction at an ATM machine is an exponential random variable with mean of 2 minutes. This means that l=2. So,
E(X) = 1/ l =1/2
VAR(X) = 1/ l^2 =1/4
STD(X) =1/ l= 1/2
The probability that it takes less than 3 minutes to complete a transaction is
P(X<3) = P(X£ 2)=F(2)=1-exp(-2*2)= 0.982
The probability that it takes more than 4 minutes to complete a transaction is
P(X>4)=1-P(X £ 4)= 1- F(4) = 1- [ 1-exp(-2*4)]=exp(-2*4)=0.000335

Example 2:
Assume that the amount of time it takes to process your order at an ice cream store is an exponential random variable with mean of 2.2 minutes.
Solution

Example 3:
Let X and Y be independent exponential random variables with E(X)=3 and E(Y) =4.6
E(X+Y)= E(X)+ E(Y)=3+4.6= 7.6
VAR(X+Y)= VAR(X)+ VAR(Y)=(3)^2 +(4.6)^2= 9+21.16=30.16
E(X)=1/l =3 implies that l=1/3 so f(x) =(1/3) exp(-x/3)
E(Y)=1/l =4.6 implies that l= 1 / 4.6 so f(y)=(1/4.6) exp(-y/4.6)
Since X and Y are independent, f(x,y) can be found simply by multiplying f(x) and f(y).So,
f(x,y)= (1/3) exp(-x/3) * (1/4.6) exp(-y/4.6)= (1/13.8) exp(-x / 3) exp(-y / 4.6)
where 0<x<¥ and 0<y<¥
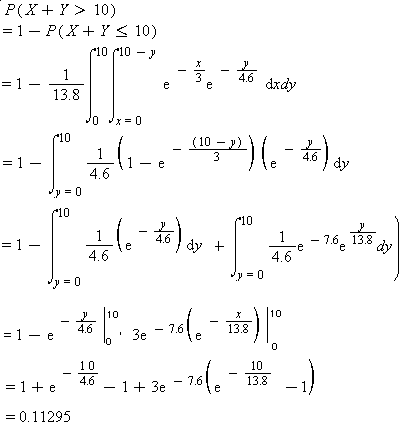


Solutions
Solution to Example 2
l=2.2
E(X) = 1/ l =1/2.2 =0.45
VAR(X) = 1/ l^2 =1/(2.2)^2=0.21
STD(X)=1/ l= 0.458= 0.46
The probability that it takes less than or equal to 2 minutes to process your order is
P(X£ 2)=F(2)=1-exp(-2.2*2)= 0.9877
The probability that it takes more than 3 minutes to process your order is
P(X>3)=1-P(X£3)= 1- F(3) = 1- [ 1-exp(-2.2*3)]=exp(-2.2*3)=0.0014

Solution to Example 4
E(X)=4 and E(Y) =5.1
E(X+Y)= E(X)+ E(Y)= 4+5.1= 9.1
VAR(X+Y)= VAR(X)+ VAR(Y)=(4)^2 +(5.1)^2= 42.01
Find the joint probability distribution of f (x,y):
E(X)=1/l =4 implies that l=1/4 =0.25
So f(x) =(1/4) exp(-x/4) and
E(Y)=1/l =5.1 implies that l= 1 / 5.1 =0.196=0.20
So f(y)=(1/5.1) exp(-y / 5.1)
Since X and Y are independent, f(x,y) can be found simply by multiplying f(x) and f(y). So,
f(x,y) = (1/4) exp(-x / 4) * (1/ 5.1) exp(-y / 5.1)= (1/20.4) exp(-x / 4) exp(-y / 5.1) where 0<x<¥ and 0<y<¥
So a= 20.4 , b=4 and c=5.1
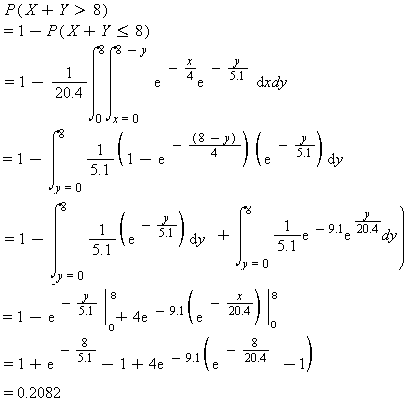

Help!
When the Web brower is opened, scroll to the bottom of the page until you find a drop down box that says Select Applet. Choose Exponential Probabilities and click Open!. When the applet opens you can enter in values for l, X0 and/or X1. Press Calculate! and the probability, pdf function and cdf function will be displayed on your screen. Enjoy!
