|
Example 1 |Example 2 | Example 3 |Example 4 |Useful Web Resources| Solutions
Definition 6.2-1
A random variable X is has the normal distribution if the probability density function is

-
The normal distribution is frequently called bell or mound-shaped
-
u and s are the expected value and standard deviation of the random variable X
-
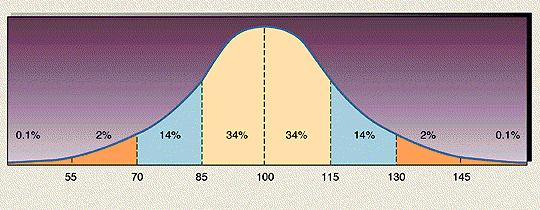
The normal distribution is symmetric about u, with half the probability lying above and half lying below u.
-
68% of the probability of the normal distribution falls within one standard deviation of the mean
-
Just over 95% of the probability of the normal distribution falls within two standard deviation of the mean
*www.has.vcu.edu/psy/ psy101/forsyth/measure/3.htm
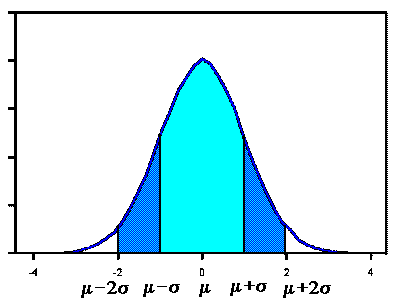
Table 4 in Appendix A gives values of the cumulative distribution function of the normal distribution with a mean of 0 and standard deviation of 1. This is called the standard normal, and denote the corresponding random variable as Z.
*http://www.stat.yale.edu/Courses/1997-98/101/normal.htm

Example 1:
Let Z be a standard normal random variable. Then P(Z £ 2.03) is found as the entry in Table 4 in Appendix A , in the row labeled 2.0 and the column labeled 0.03. So,
P(Z£ 2.03) = F(2.03)=0.9788
P(Z >1.44) = 1-P(Z£ 1.44) =1-0.9251=0.0749
P( -2.1 < Z < 3.4) = P(Z< 3.4) -P(Z £ -2.1)
=P(Z< 3.4) -[1-P(Z £ 2.1)]
=F(3.4)- 1 + F( 2.1)
=0.99966-1+ 0.98210
= 0.98177
Round all answers to 4 decimal places
Z distribution Table
Solution

Theorem 6.2-1:
If X has a normal distribution with mean u and standard deviation s , then the random variable Z=(X-u) / s has a standard normal distribution.
Example 2:
Let u = 2 and s = 4. What is P(X £ 10)?
P(X £ 10) = P[Z £ (10-2)/4]
= P(Z £ 2)=F(2)
=0.9772
What is P(X > 11)?
P(X > 11)= 1- P[Z £ (11-2)/4 ]
=1-F(2.25)=1-0.9878
=0.0122
What is P(2£ X £ 5)?
P(2£ X £ 5)= P(X£ 5)-P(X£ 2)
=P[Z £ (5-2)/4 ] -P[Z £ (2-2)/4 ]
=P(Z £ 0.75) -P(Z £ 0)
=F(0.75) -F(0)
= 0. 7734-0.5
=0.2734
Let u = 3 and s = 2. Complete the table below.
Z distribution Table
Solution

Theorem 6.2-2:
If X has a normal distribution with mean u and standard deviation s , then Y=a +bX has a normal distribution with mean u(y)= a+bu and standard deviation s(y) = |b|s
Theorem 6.2-3:
Let X have a binomial distribution with parameters n and p. For large n, X will have an approximate normal distribution with mean u=np and standard deviation s= sqrt[ np(1-p) ]
Example 3 :
Let X have a binomial distribution with parameters n=30 and p=0.2. P(X £ 24)
Using Theorem 6.2-3 we know that for large n X will have an approximate normal distribution with u = 30*0.2= 6 and s =30*(0.2)*(0.8)=4.8. So,
P(X £ 21) = P[Z £ (21-6)/4.8]
= P(Z £ 3.125)=F(3.13)
=0.9991
Find the following proabilities. Round all answers to 2 decimal places.
Z distribution Table
| n |
300 |
150 |
60 |
| p |
0.5 |
0.25 |
0.1 |
| Probability |
P(X£160) |
P(X>50) |
P(7£ X £ 9) |
| Answer |
|
|
|
Solution

Example 4:
Let X be a random variable. ln(X) is normally distributed with u=4.1 and s= 2.3.
P(X > 11)= P[ln(X)> ln(11) ]
=P[ln(X)> 2.40 ]=P[Z> (2.4-4.1)/2.3] =P[Z>-0.74] =P[Z£0.74]=0.7704
Let X be a random variable. ln(X) is normally distributed with u=2.7 and s= 1.05.
Solution
 Use the following applet to explore the Normal Distribution! Use the following applet to explore the Normal Distribution!

Useful Web Resources
SurfStats

Solutions
Solution to Example 1
P(Z£ 2.11) = F(2.11)= 0.9826
P(Z >2.3)= 1-P(Z£ 2.3) =1-0.9893=0.0107
P( 2 < Z < 3) = P(Z< 3) - P(Z £ 2)]
=F(3) - F( 2)
=0.9987 - 0.9772 = 0.0215
P(-1< Z < 1.1) = P(Z< 1.1) - P(Z £ -1)]
= P(Z< 1.1) - [1- P(Z £ 1)]=F(1.1)- 1 + F( 1)
=0.8643-1+ 0.8413 = 0.7056

Solution to Example 2
Let u = 3 and s = 2. What is P(X £ 5)?
P(X £ 5) = P[Z £ (5-3)/2]
= P(Z £ 1)=F(1)
=0.8413
What is P(X > 7)?
P(X > 7)= 1- P[Z £ (7-3)/2 ]
=1-F(2)=1-0.9772
=0.0228
What is P(2£ X £ 6.5)?
P(2£ X £ 6.5)= P(X£ 6.5)-P(X£ 2)
=P[Z £ (6.5-3)/2 ] -P[Z < (2-3)/2 ]
=P(Z £ 0.75) -P(Z £< -0.5)
=F(1.75) - [1-F(0.5)]
= 0.9599-1+0.6915
=0.6514

Solution to Example 3
a)
X has a binomial distribution with parameters n=300 and p=0.5. P(X £ 130)
Using Theorem 6.2-3 we know that for large n X will have an approximate normal distribution with u = 300*0.5= 150 and s =300*(0.5)*(0.5)=75 .So,
P(X £ 160) = P[Z £ (160-150)/75]
= P(Z £ 0.13)
=F(0.13)
=0.5517
=0.55
b)
X has a binomial distribution with parameters n=150 and p=0.25. P(X >50)
Using Theorem 6.2-3 we know that for large n X will have an approximate normal distribution with u = 150*0.25= 37.5 and s =150*(0.25)*(0.75)= 28.125 .So,
P(X > 50) =1- P[Z £ (50-37.5)/28.125]
=1-P(Z £ 0.44)=1-F(0.44)=1-0.67
=0.33
c)
X has a binomial distribution with parameters n=60 and p=0.1. P(4£ X £ 5)
Using Theorem 6.2-3 we know that for large n, X will have an approximate normal distribution with u = 60*0.1= 6 and s =60*(0.1)*(0.9)= 5.4 .So,
P(7£ X £ 9)= P(X £ 9)-P(X £ 7)
=P[Z £ (9-6)/5.4 ] -P[Z < (7-6)/5.4 ]
=P(Z £ 0.56) -P(Z £0.19)
=F(0.56) - F(0.19)]
=0.7123-0.5753
=0.137
=0.14

Solution to Example 4
P(X £ 4)= P[ln(X) £ ln(1.39) ]
=P[ln(X) £ 1.39 ]
=P[Z£ (1.39-2.7)/1.05]
=P[Z£ -1.25]
=1- P[Z£1.25]
=1-0.8944
=0.1056

.
.
|