|
Example 1 |Example 2 | Example 3 |Useful Web Resources| Solutions
Counting processes arise naturally in dealing with the number of outcomes of various kinds that occur across time Defintion 7.1-1:
A stochastic process is called a counting process if
i) The possible states are the non-negative integers.
ii) For each state i the only possible transitions are
i --> i, i--> i+1 , i--> i+2 , ...
Defintion 7.1-2:
A counting process is said to be a Bernoulli counting process if
i) The number of successes that can occur in each frame is either 0 or 1
ii) The probability p that a success occurs during any frame is the same for all frames
iii) Successes in non-overlapping frames are independent of one another
Theorem 7.1-1:
Let X(n) denote the total number of successes in a Bernoulli counting process at the end of the nth frame, n=1,2,3.... Let the initial state be X(0)=0. The probability distribution of X(n) is the binomial
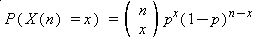
If l denotes the expected number of successes in a unit of time, and n is the number of frames in this unit of time, then
The constant l is called the rate of success, and is estimated by
If there are n frames in the unit of time and we let the frame length, denoted by D, be expressed in the same unit as l (seconds, minutes, hours,etc.), then D=1/n. Moreover,

Example 1:
A teen help line recieves on average l =5 calls per hour. Suppose that the number of calls can be modeled by a Bernoulli counting process with 2-minute frames. Since l is in hours, we have 30 2-minute frames in an hour. So D= 1/n = 1/30. The probability of a call during a 2 minute frame is p = l D = 5/30= 1/6
Assume the teen help line recives on average l = 3 calls per hour. The number of calls can be modeled by a Bernoulli counting process with 6-minute frames. What is p?
Solution

Theorem 7.2-1:
Let Y denote the number of frames from one success to the next. The probability mass function of Y is
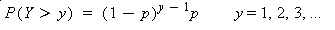
This is the geometric distribution discussed in Section 3.2 with u = 1/p and s^2 = (1-p) / p^2
Example 2:
A customer help line recieves on average l =7 calls per hour. Suppose that the number of calls can be modeled by a Bernoulli counting process with 3-minute frames. What is the probability that there is more than 1 hour from one call to the next?
Solution:
Since l is in hours, we have 20 3-minute frames in an hour. So D= 1/n = 1/20. The probability of a call during a 2 minute frame is p = l D = 7/20 = 0.35. Since there are 20 frames in an hour, we want to find P(Y>20). We know that in general,
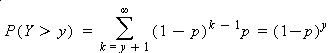
P(Y>20) =(0.65)^20=0.00018
u=1/p =1/0.35 =2.86 frames
s^2 = (1-p) / p^2 = 0.65/ (0.35)^2 =5.3
s = sqrt(5.3)=2.3
A customer help line recieves on average l =4 calls per hour. Suppose that the number of calls can be modeled by a Bernoulli counting process with 1-minute frames. What is the probability that there is more than 1 hour from one call to the next?
Solution

Theorem 7.1-3:
If T is the time from one success to the next in a Bernoulli counting process, then
E(T)= 1/ l
VAR(T) = (1-l D) / l^2
For small D, VAR(T) is apporximatley 1/ l^2
Example 3 :
Suppose that the number of boats arriving at a dock is a Bernoulli counting process with a rate of l=3 per hour and the frame length is D = 1/30 hour. So,
E(T)= 1/ l =1/3 = 0.33
VAR(T) = (1-l D) / l^2 = [1-(3/30)] / 3^2 =0.1
Suppose that the number of boats arriving at a dock is a Bernoulli counting process with a rate of l=6 per hour and the frame length is D = 1/12 hour.
Round all answers to 2 decimal places
Solution

Stochastic Processes

Solutions
Solution to Example 1
The teen help line recives on average l = 3 calls per hour. The number of calls can be modeled by a Bernoulli counting process with 6-minute frames. Since l is in hours, we have 10 6-minute frames in an hour. So D= 1/n = 1/10. The probability of a call during a 6 minute frame is p = l D = 3/10= 0.3

Solution to Example 2
Since l is in hours, we have 60 1-minute frames in an hour. So D= 1/n = 1/60. The probability of a call during a 1 minute frame is p = l D = 4/60 = 0.07. Since there are 60 frames in an hour, we want to find P(Y>60).
P(Y>60) =(0.93)^60=0.0129
u=1/p =1/0.07 = 14.3 frames
s^2 = (1-p) / p^2 = 0.93/ (0.07)^2 =189.8
s = sqrt(189.8)=13.8

Solution to Example 3
E(T)= 1/ l =1/6 = 0.17
VAR(T) = (1-l D) / l^2 = [1-(6/12)] / 6^2 =0.0139=0.01

.
.
|