|
Example 1 |Example 2 | Example 3 |Useful Web Resources| Solutions
Defintion 7.2-1:
Let N(t) denote the number of successes in the interval [0,t]. Assume that N(t) is a continuous-time counting process and that the count begins at zero.
N(t) is said to be a Poisson process if
i) Successes in non-overlapping intervals occur independently of one another
ii) The probability distribution of the number of successes depends only on the length of the interval and not on the starting point of the interval.
iii) The probability of x successes in an interval of length t is
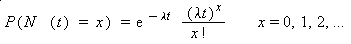
where l is the expected number of successes per unit of time.
Example 7.2-1:
Suppose transmission errors in sending data over a telephone line is a Poisson process with a rate of l= 2.1 errors per minute.
What is the probability of having no errors in 3 seconds of transmission ?
Solution:
The time in question is t = 3/60 =1/20 minute , and the expected number of errors is lt = 2.1/20= 0.105. So,
P( N (1/20) =0 ) = exp(-0.105)[(0.105)^0] / 0! =0.9
What is the probability of having 2 or fewer errors in 6 seconds of transmission ?
Solution:
The time in question is t = 6/60 =1/10 minute , and the expected number of errors is lt = 2.1/10= 0.21. So,
P( N (1/10) £ 2 ) = exp(-0.21)[(0.21)^0] / 0!
+ exp(-0.21)[(0.21)^1] / 1!
+exp(-0.21)[(0.21)^2]/2!
=0.81058+ 0.17022+ 0.01787
=0.99867
Example 1:
Suppose transmission errors in sending data over a telephone line is a Poisson process with a rate of l= 1.7 errors per minute. Find the probability that there are no errors in 4 seconds of transmission.
Solution
Example 7.2-2:
The number of requests for computer searches at a certain library during the evening hours is a Poisson process with l=8 requests per hour.
What is the probability that there are more than 4 request for service in 15 minutes.
Solution:
The time in question is t = 15/60 =1/4 hour , and the expected number of errors is lt = 8/4= 2. Using Table 3 of Appendix A,
P( N(1/4) >= 4 ) = 1- P( N(1/4) £ 3)
= 1- 0.8571
=0.1429
What is the mean and standard deviation of the number of requests in 2.5 hours?
Solution:
2.5 hours is 150 minutes, or 10 15-minute frames. So the mean number of requests in 2.5 hours is lt = 8(10)= 80
s= sqrt(lt) = sqrt(80)= 8
Example 2:
The number of requests for computer searches at a certain library during the evening hours is a Poisson process with l=12 requests per hour. Find the probability that there are more than 8 request for service in 30 minutes.
Poisson Cumulative Distribution Function
t |
|
lt |
|
P( N(1/2) >= 8 ) |
|
Mean number of requests in 2 hours |
|
s |
|
Solution
Theorem 7.2-1:
Let T be the time between consecutive successes in a Poisson process with rate
l. Then T has an exponential distribution with probability density function
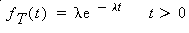
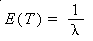
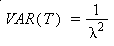
Example 7.2-3:
The number of planes taking off from an airport is a Poisson process with an expected value of 12 in 6 hours.
What is the probability that there are 45 minutes or less between consective takeoffs.
Solution:
If time is measured in hours, then l= 12/6 =2 per hour and t =3/4 (45 minutes is 3/4 of an hour) . So,
P(T £ 0.75) = 1-exp[-(2)(0.75)] = 0.78
What is the expected value and standard deviation of the time between landings?
Solution:
E(T) = 1/ l = 1/2 hours
s= 1/ l^2 =1/4 =0.25 hours
Example 3:
The number of planes taking off from an airport is a Poisson process with an expected value of 15 in 4 hours. Find the probability that there are 20 minutes or less between consecutive takeoffs.
Please round all answers to 2 decimal places.
l |
|
t |
|
P(T £ 1/3) |
|
E(T) |
|
VAR(T) |
|
Solution
 Explore the Poisson Process, by clicking on Poisson Experiment when the link opens. Enter the value of l for r.
Poisson Process- Wikipedia
Solutions
Solution to Example 1
1: The time in question is t = 4/60 =1/15 minute ,
2: The expected number of errors is lt =(1.7)/15= 0.113
3: P( N (1/15) =0 ) = exp(-0.113)[(0.113)^0] / 0! =0.8932
4: P( N (1/15) £ 2 ) = exp(-0.113)[(0.113)^0] / 0!
+exp(-0.113)[(0.113)^1] / 1!
+exp(-0.113)[(0.113)^2] / 2!
=0.8932+ 0.1009+ 0.0057
=0.9998
5: The time in question is t = 4 minutes
6: The expected number of errors is lt = (1.7) *4 = 6.8.
7: P( N (4) £ 2 ) = exp(-6.8)[(6.8)^0] / 0!
+ exp(-6.8)[(6.8)^1] / 1!
+ exp(-6.8)[(6.8)^2 / 2!
=0.0011+ 0.0076+ 0.0258
=0.0345
Solution to Example 2
1: The time in question is t = 30/60 =1/2 hour
2: The expected number of errors is lt = 12/2= 6
3: Using Table 3 of Appendix A
P( N(1/2) >= 8 ) = 1- P( N(1/2) £ 7)
= 1- 0.7440
=0.256
4: 2 hours is 120 minutes, or 4 30-minute frames. So the mean number of requests in 2 hours is lt = 12(4)= 48
5: s= sqrt(lt) = sqrt(48)= 6.9
Solution to Example 3
1: If time is measured in hours, then l= 15/4 =3.75 per hour
2: t =1/3 =0.33 (20 minutes is 1/3 of an hour)
3: P(T £ 1/3) = 1-exp[-(3.75)(1/3)] = 0.71
4: E(T) = 1/ l = 1/3.75= 2.67 hours
5. VAR(T) = 1/ l^2 =1/(3.75)^2 =0.07 hours
.
.
| 
