|
Example 1 |Example 2 | Useful Web Resources| Solutions
Defintion 7.3-1:
Let Ti, i =1,2, ..., denote the interarrival times in a Poisson process with rate l. The Ti's are independent exponential random variables each with mean u = 1/ l.
This theorem is useful in simulating a Poisson proccess. The interrarival times are T1,T2, ... , Tn are simulated as n exponential random variables. The first n successes occur at times T1, T1+T2, ...,T1+ T2 + ...+Tn.
Theorem 7.3-2:
The cumulative distribution function of the waiting time Wn is
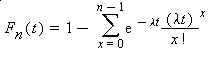
where n is the number of successes, and t is time.
This is also called the Erlang distribution. The probability density function of this distribution is
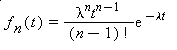
The Erlang distribution is a special case of the gamma distribution with a = n and b= 1/ l.
Example 7.3-2:
The number of thunderstorms occuring in a city during the summer is a Poisson process with rate l=0.45 per week.
What is the probablility that the waiting time for 2 storms is 3 days?
Solution:
This is also the probablility that there are zero or one storm in 3 days. So lt = (0.45)(3/7)= 0.19 and we have
P(W2 >3)= P( N(5) £ 1)
= exp(-0.19)[(0.19)^0] / 0! + exp(-0.19)[(0.19)^1] / 1! =0.98
There is about a 98% chance that we will have to wait more than 3 days for two storms

Example 1
The number of thunderstorms occuring in a city during the summer is a Poisson process with rate l=0.78 per week.
What is the probability that the waiting time for 3 or more storms is more than 6 days?
Round all answers to 2 decimal places
Solution

Theorem 7.3-3:
The mean and variance of the waiting time random variable Wn are
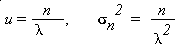
Example 2:
A: Refer to Example 7.3-2 above.
Find the mean and standard deviation of the time to observe two thunderstorms.
Round all answers to 2 decimal places
B: Refer to Example 1 above.
Find the mean and standard deviation of the time to observe 3 thunderstorms.
Round all answers to 2 decimal places
Solution

Erlang Distribution-Wikipedia
Statistical Distributions- Erlang

Solutions
Solution to Example 1
t =6/7 = 0.86
So lt = (0.78)(6/7)= 0.67 and we have
P(W3 > 6)= P( N(6) £ 2)
= exp(-0.67)[(0.67)^0] / 0! + exp(-0.67 )[(0.67)^1] / 1! + exp(-0.67)[(0.67)^2] / 2! = 0.511708577+0.342844747 + 0.14485299 =0.9694 =0.97
There is about a 97% chance that we will have to wait more than 6 days for 3 storms

Solution to Example 2
A:
m = n / l =2/ 0.45 = 4.44
s = sqrt (2) / 0.45 = 3.14
B:
m = n / l =3/ 0.78 =3.85
s = sqrt (3) / 0.78 = 2.22

|