|
Example 2 | Example 4 |Useful Web Resources| Solutions
Theorem 8.1-1:
Let X1, X2, ..., Xn be independent, normally distributed random variables with E(Xi) = mi and STD (Xi)= si for i=1,2, ..., n. Then the sum X =X1 + X2 + ...+Xn has a normal distribution with the following mean and standard deviation:
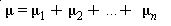
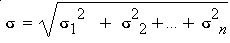
Example 1:
Let X1 and X2 be random variables where m1= 3.5, m2 = 5.6 , s1= 1.1 and s2 =2.3.
X= X1 + X2. If X1 and X2 are independent the mean and standard deviation of X are as follows:
m = 3.5 + 5.6= 9.1
s = sqrt[ (1.1)^2 + (2.3)^2 ] =6.5
The probability that X is greater than 8 is:
P(X > 8) = 1- P(X £ 8)
=1-P( Z £ (8-9.1)/6.5)
=1- P(Z £-0.17)
=1 - 0.432505
=0.5675

Example 2
Let X1 and X2 be random variables where m1= 2.1, m2 = 4.6 , s1= 0.78 and s2 = 1.4.
Asumme X1 and X2 are independent, and X= X1 + X2. Find the mean , standard deviation of X.
Round all answers to 1 decimal place
Solution

Theorem 8.1-1b:
An important special case of Theorem 8.1-1 occurs when the Xi's are a random sample. If the mean and standard deviation of the Xi's are denoted by m and s respectively, then the sum of n such independent, normally distributed random variables has a normal distribution with mean m + m + ... + m = nm and a standard deviation sqrt ( s ^2 + s ^2 + ... + s ^2 ) = s sqrt(n).
Example 3:
Refer to Exercise 8.1-3 onpage 329, and consider these new these new values.
|
Mean |
Standard Deviation |
| 1. Unload the equipment |
4 |
1 |
| 2. Unroll the sail and slide it on the mast |
2 |
2 |
| 3. Downhaul the sail |
1.5 |
0.5 |
| 4. Adjust the boom length and attach it to mast |
2.5 |
2 |
| 5. Outhaul the sail |
2 |
1.5 |
| 6. Adjust the battens |
3 |
0.5 |
What is the expected value and standard deviation of T?
Solution:
T =T1 +T2 + T3 + T4 + T5 + T6 . Since the times are independent random variables,
E(T)= E ( T1 +T2 + T3 + T4 + T5 + T6) = E(T1)+ E(T2) + E(T3) + E(T4) + E(T5) + E(T6) = 4 + 2 + 1.5 +2.5 +2+ 3 =15
VAR(T) = VAR( T1 +T2 + T3 + T4 + T5 + T6)
= VAR(T1)+ VAR(T2) + VAR(T3) + VAR(T4) + VAR(T5) + VAR(T6)
=1+ 4 + 0.25 + 4 + 2.25 + 0.25
=11.75
STD(T)= sqrt(11.75) =3.4
Within what range should we expect the total time to fall?
Solution:
To find the range we need to calculate E(T) +/- 2STD(T). So the range is,
[E(T) -2STD(T), E(T) + 2STD(T)] = [15 -2(3.4), 15 +2(3.4)]= [8.2 , 21.8]
Assume that the random variables have a normal distribution. What is the probability that the it will take less than 12 minutes to rig a sail?
Solution:
P(T < 12) = P [Z < (12-15)/3.4] = P(Z <-.88)= 1- F(88) =1- 0.8106=0.1894

Example 4:
Consider Exercise 8.1 on page 328. The means and standard deviations for the time to complete 400 meters in a 1600-meter relay race involving four runners are given in the following table. Notice they are different from the values given in the book. Let T denote the total time to run the race.
Runner |
Mean Time to Complet 400 Meters (seconds) |
Standard Deviation (seconds) |
1 |
60 |
1 |
2 |
54 |
1.5 |
3 |
50 |
2 |
4 |
57 |
1 |
Complete the chart below:
E(T) |
|
STD(T) |
|
What is the range you would expect the total time to fall ? |
|
P(X< 215) |
|
Solution

Sums of Random Variables

Solutions
Solution to Example 2
A: m = 2.1 + 4.6= 6.7
B: s = sqrt[ (0.78)^2 + (1.4)^2 ] =2.6
C: P(X < 9) = P(X £ 8)
=P( Z £ (8-6.7) / 2.6)
=P(Z £ 05)
=F( 0.5)
=0.6915
=0.7

Solution to Example 4:
A:
T =T1 +T2 + T3 + T4 . Since the times are independent random variables,
E(T)= E ( T1 +T2 + T3 + T4 ) = E(T1)+ E(T2) + E(T3) + E(T4) = 60 + 54 + 50 + 57=221 seconds
B:
VAR(T) = VAR( T1 +T2 + T3 + T4)
= VAR(T1)+ VAR(T2) + VAR(T3) + VAR(T4)
=1+ 2.25 +0.25 +4 + 2.25 + 0.25
=10 seconds
STD(T)= sqrt(10) =3.2 seconds
C: [E(T) -2STD(T), E(T) + 2STD(T)] = [221 -2(10), 221 +2(10)]= [201 , 241]
So the upper bound is 241 and the lower bound is 201
D: P(T < 215) = P [Z < (215-221) / 3.2] = P(Z <-1.88)= 1- F(1.88) =1- 0.9699=0.0301 =0.03

.
.
|