Electrochemical reactions meet the necessary conditions for pattern formation, in that they form a system which operates far from thermodynamic equilibrium with appropriate feedback mechanisms and communication between the constituent elements. Although experimental observations of instability in electrochemical systems have long been noted[1], it was not until the 1990’s that theoretical foundations on origin of oscillatory behavior observed earlier in many electrochemical systems were studied and identified [2-5].

Electrochemical reaction systems couple transfer processes with complex reactions, both of which are usually highly nonlinear, and can exhibit a variety of dynamical behavior, ranging from harmonic to chaotic oscillations[6-8]. Studying the dynamics of electrochemical systems has some advantages over other nonlinear dynamical systems. Firstly, the main parameters in electrochemistry, potential and current, are relatively easier to control and measure than parameters found in other systems. Secondly, the time scale of electrochemical oscillations is relatively short compared to other types of oscillators, which allows rapid data acquisition and analysis. Thirdly, the patterns formed on the reacting surface, which is the working electrode, can easily be recognized and controlled by several techniques, including the use of addressable electrode arrays.

Collective dynamics, giving rise to pattern formation, can be observed in prototype nonlinear models such the one proposed by Alan Turing [9], where the individual entities are reaction sites and the coupling is through diffusion or convection[10]. In the case of electrochemical reactions, the driving variable for the reaction dynamics is the double layer potential, the voltage drop over the electrode/electrolyte interface, while spatial coupling is made possible through transport processes and external control mechanisms.

Generally, pattern formation due to reaction-diffusion can be described by looking at the temporal evolution of concentration described through[11],

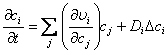                                          (2.14)

For ci representing the concentration of all the time variant species i in the system, and j representing all the species whose reactions have an effect on ci. υi denotes the overall rate of change of ci due to reactions, whose partial derivative with respect to any cj may be a nonlinear function, like that of equation 2.13. The first component on the right hand side of the equation describes the activator-inhibitor dynamics which can give rise to temporal instabilities while concentration gradients in the second part will provide the ability for spatial locations to communicate with each other through diffusion transport enabling a system described through the above equation to maintain and create spatial patterns.

For electrochemical systems, a mechanistic explanation of activator-inhibitor dynamics such as nickel in sulfuric acid used in this report, is based on reaction rates and surface dynamics [12]. For example, a simple oscillatory feedback mechanism suggested in early theoretical description of instability in Fe/H2SO4 systems, can be demonstrated through pH dependence of potential across the active-passive transition region[13-15]. As the metal of the working electrode dissolves protons migrate away from the working electrode. The Flade potential, described in the following sections, shifts to a more cathodic value, and passive film formation sets in. Due to passivation, the current drops. The protons now diffuse back to the working electrode, and the Flade potential shifts to a more anodic value and the metal reactivates. Here, there is an interplay between diffusion and migration of protons in front of the working electrode as a mean of mass transport and together they work to allow oscillations to occur.  Diffusion is due to proton concentration gradient in the diffusion layer while migration of protons away from the surface of the working electrode is due to the electrical field.

In activator-inhibitor type electrochemical systems the potential takes on the role of the activator while the inhibitor is a chemical quantity, that is, the concentration of the electroactive species or the coverage of the electrode. Spatial inhomogeneities in activator and inhibitor can then induce migration and diffusion fluxes respectively, which in turn lead to the occurrence of electrochemical pattern formation. The main difference from a reaction diffusion system is that, in contrast to diffusion, migration represents a long-range spatial coupling [16]. Furthermore the transport mechanism in electrochemical systems is mostly influenced by migration rather than diffusion[17]. In this way, local perturbations in the double layer potential are mediated through the electric field in the liquid phase[18]. Thus, spatial inhomogeneities in the double layer potential are felt not only by nearest neighbors but by a whole range of neighboring sites.

The equations which will be looked at more closely in the next section are related to reaction-diffusion type dynamics since they can be described by a local function and a spatial coupling term. Furthermore, global coupling is routinely present in electrochemical experiments and it could play a stabilizing or destabilizing role in the dynamics, acting as an activator as well as an inhibitor depending on the electrochemical reaction under consideration[19-21]. The strength of this global coupling may be readily varied since it is introduced by an external control circuit[22].

We start a closer look by considering the fundamental electrochemical kinetics of metal electrode dissolution. We will then extend the theory and consider a model based on coupled differential equations that take time variance of defining parameters into account which will assist in building a conceptual background for observed experimental instabilities.

1.1.1       Electrodissolution of metals

The existence of electrochemical electrode potential is due to a process similar to that of solid state junctions. When two metals with dissimilar workfunction potentials are brought together, electron and holes will flow in the established potential field until an opposite potential due to excess charge is established to oppose this otherwise continuous current. In an electrochemical cell, as illustrated in Figure 5, when a metal electrode is immersed in liquid electrolyte, ions from the metal surface will dissolve until a junction potential is created due to the charge imbalance. This potential , under standard conditions is specific to each metal dissolution process and is related to the free enthalpy of cell reaction by considering that the during the completion of the cell reaction the transfer of charge nF is affected. Under equilibrium conditions this potential is influenced by metal ions activity in the electrolyte as can be derived from basic thermodynamic principles and is given by the celebrated Nernst equation in Figure 5.

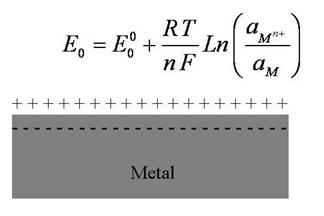
Figure 5 Built-up of electrical charge in the electrolyte

 

In the following section, we will extend this simple model to consider the effects of applied over potential and the spatially extended description of the charge within the electrolyte.

 

1.1.1.1  Electrode kinetics

 

We will first consider electrode kinetics due to charge transfer polarization and the effect of changing the rest potential which induces a net current to pass through the electrode. The rate of electrochemical reaction υ can be defined as the difference between the rate of anodic reaction(oxidation) and the cathodic reaction (reduction) at the electrode surface.

                                          (2.15)

with cs representing the surface concentration and k the rate constant. The rate constant is related to the activation energy and thus influenced by an external potential. The rate can be predicted by Arrhenius equation,

 and           (2.16)

At equilibrium the reaction rates are equal and no net current passes through the electrode. The equal anodic and cathodic currents at equilibrium are the exchange current densities, indicated as i0 in Figure 10. However with the addition of an overpotential Δφ, energy of ions in the metal surface are changed by zfΔφ and one reaction becomes more thermodynamically favorable. We can write out the relation between the Gibbs energy of activation to that of the applied electrode potential

 

                             (2.17)

 with 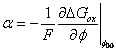for representing the anodic transfer coefficient which describes the  change in the energy of activation with Gibbs energy, hence determining the dependence of current on electrode potential and giving the variation of Gibbs energy of activation with potential.  Also

 

                          ( 2.18)

 

Where 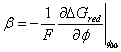for  representing the cathodic transfer coefficient, with . Since the current density j associated with a reaction is j=Fwe can write the equation, also known as the Butler-Volmer equation, describing the relation between current density and polarization from the open circuit potential Ф00 as,

             (2.19)

With, and if we introduce the overpotentialthe Butler-Volmer equation can be written as

                                    (2.20)

for representing the exchange current density. If mass transfer is not a limiting factor in the reaction, that is if we assume the surface concentration is dictated by equilibrium conditions, we can use the Nernst equation for the concentration. Concentration induced polarization is considered in the next section. In the very close proximity of the exchange current, that is for very small overpotentials, the Butler-Volmer equation can be expanded with a Taylor series and with only the first term current can be approximated as a linear function of overpotential,

                                                   (2.21)

However as the overpotential is increased, a more important approximation can be made by considering that forward reaction exponential in the Butler-Volmer equation becomes insignificant compared to the reverse reaction,

                               (2.22)

And the current is given by logarithmic relationship,

                                           (2.23)

Which solving for overpotential gives the Tafel equation

                                                 (2.24)

An experimental example of current with the application an anodic overpotential to nickel electrode in sulfuric acid electrolyte is illustrated in Figure 6. The logarithmic graph shows the linear Tafel region and is often better suited to demonstrate the wide rang of currents encountered during metal electrodissolution.


 

 

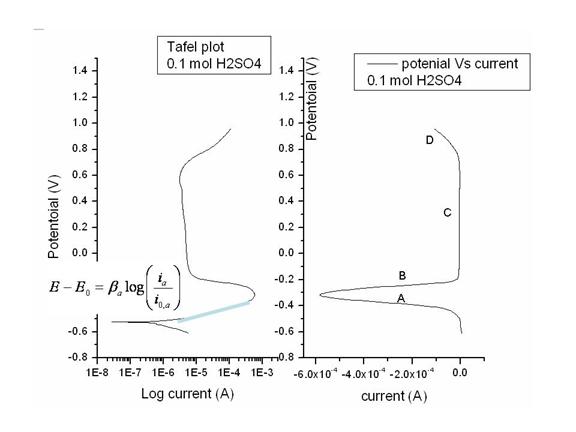
Figure 6 Electrodissolution polarization curve

 

Polarization curves such as the one in Figure 6 help identify the kinetics at various potentials under steady state condition and this information as will be discussed in section 4 is necessary for establishing base parameters for instability experiments. It should be mentioned here that Figure 6 is actually a mixed polarization curve, which is discussed in the next section (see Figure 10), but with increasing overpotential, anodic nickel dissolution dynamics dominate. As pointed out in Figure 6 the regions of interest which help identify the underlying dynamics are:

 

  1. As the potential is increased above the corrosion potential, metal electrode is dissolved according to the thermodynamic laws discussed, which give rise to the Tafel equation. Above the linear Tafel region other polarization effects such as diffusion, decrease the rate current increase with increasing potential. Furthermore, processes such deposition of salt or formation of porous oxide can further complicate the picture as is illustrated in Figure 7. since the layer formed is resistive to current flow, current density will increase on localized surfaces, while the total observed current will either stay constant or decrease. The salt can eventually become displaced by activating ions and dissolution will continue to a maximum current occurring at the Flade potential
  2. The Flade potential indicates the onset of passivation layer formation on the electrode.
  3. The passivation potential is reached when current settles at a steady state, beyond which further corrosion is prevented by the protecting oxide layer that covers the entire surface. In the passivation region, the dissolution current falls to a very low value. The small anodic current which does exist in this region is due to the passivation layer dissolving in the electrolyte, which must be compensated by a slow oxidation of the metal electrode. Temporal patterns which are reported here and occur in this region are particularly attractive as the small current densities prolong the electrode life
  4. Onset of pitting potential where localized erosion of oxide layer occur
  5. On further increasing of the potential a transpassive current flows due to oxygen evolution. Here, anodic oxidation of the passivation layer becomes thermodynamically favorable allowing for the dissolution of the working electrode to continue along with generation of oxygen.

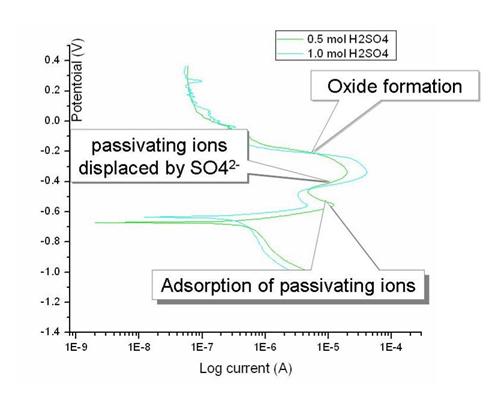
Figure 7 Adsorption passivation

 

1.1.1.2  Effect of double layer structure on electrochemical reaction rate

 

A phase boundary is formed when a metal electrode is brought into contact with the liquid electrolyte. The subsequent rearrangement of electric charges to achieve equilibrium in each phase due to charge transfer and adsorption of ions among other factors gives rise to a structured and distributed electric potential difference in the boundary layer known as the double layer. As illustrated in Figure 8, at a given potential hydrated ions will accumulate in front of the working electrode and will cause an equal excess charge in the metal. The charge layer in the metal is only of about 0_ 1angstrom thickness (Figure 8 is not to scale).

The solution side of the double layer can extend up to some 10 nm and can be thought of being made of various layers. The most common model defines two layers: The inner Helmholtz layer is given by the distance of the plane passing the centre of the specifically adsorbed hydrated ions to the metal surface. The outer Helmholtz layer is defined by the distance of the solvated ions to the working electrode which are held in their structure by electrostatic forces. At higher concentrations the Helmholtz charge structure becomes increasing significant and the total double layer capacitance is given by 1/C = 1/CGC+1/CH. A diffuse layer connects the outer plane to the bulk solution. The thickness of the diffuse layer depends on the concentration of the solution. In the models employed for describing temporal instabilities in the next section, the double layer is described by a capacitor with fixed specific capacity CDL, in space and time.

The voltage drop over the double layer, denoted by fDL, in Figure 8 is the main driving force of all electrochemical processes and thus the central variable in building an electrochemical model for oscillations. The role of the potentiostat employed in generating the polarization curves described before, is to maintain a Фapplied in Figure 8 between the reference and working electrode.

Figure 8 Electrical double layer

 

We can solve for the structure of the double layer by considering

                                                 (2.25)

for representing the charge density, (x) potential obeying the Poisson’s equation. The charge density is given by

                               (2.26)

for n(x) representing the ionic density. The ionic density can be related to the potential through Boltzmann statistics which with (¥) = 0 gives

 

and

                                   (2.27)

This can be subbed into the Poisson’s equation to get a differential for the inner potential which can be linearized at <<1 to give

                                                 (2.28)

for representing the Debye inverse length. With the boundary condition of (¥) = 0 the potential can now be solved to give,

(x) = Aexp(-x)                                           (2.29)

for A=obtained from the charge balance 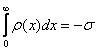 and representing the charge on the metal surface. Now the effect can be summarized as a distance dependant potential.

The double layer effects become increasingly important at low concentration electrolytes where electrostatic potential at the reaction site differs from that of the bulk. Here, even if the bulk and surface concentrations are at equilibrium, one must use the use a surface concentration  for representing the potential at the reaction site with the potential at bulk set to zero, and the c­0 the bulk concentration. Furthermore the effect of the overpotential must be changed by.

An assumption of electroneutrality in the diffuse layer and modeling the phase boundaries by a capacitor will simplify the image of potential distribution in the electrolyte in the next section.


 

 

1.1.1.3  Mass transfer polarization

 

When the concentration of reacting species at the electrode surface is lower than that of electrolyte, flux of ions becomes the rate controlling factor. As Figure 9 demonstrates, mass transfer may be due to either diffusion, which depends on concentration gradients or migration which is the movement of charged species under an electric field. Convection which is due to fluid motion is not discussed here since the electrolyte solution in our experiments was not stirred. As will be discussed in the next section mass transfer plays an important role in providing local and long range coupling and communication in pattern formation during electrochemical dissolution.

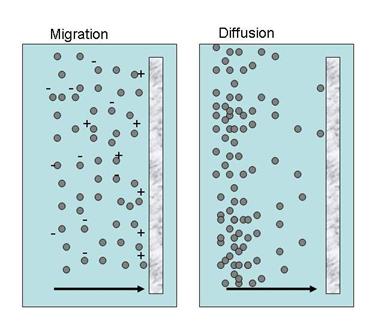
Figure 9 Mass transport in electrochemical systems

 

When the electrode processes take place according to diffusion kinetics the steady state current passing through the working electrode is given by Fick’s first law,

                                                            (2.30)

For J the diffusion flux [mol m-2 s-1], c concentration [mol m-3], D diffusion coefficient [m2 s-1] with temperature dependence of for EA activation energy for diffusion [energy (mol)-1], and c concentration [mol m-3].  is the concentration gradient in the immediate vicinity of the electrode.

The time variance of concentration plays a role in pattern formation (see Figure 17) and we can relate the time differential to concentration gradient through Fick’s second law, which can be derived from the first law of diffusion and mass balance

                                      (2.31)

or in three dimensions, considering that the diffusion coefficient does not change with coordinates. In case of steady state Fick’s second law gives linear concentration profile near the working electrode. It is therefore necessary for complex temporal behavior that the concentration exhibit a minimum second order variation with respect to spatial coordinates. In the section on theoretical basis of temporal patterns we will assume a linear change in concentration gradient for a simplified model.

Similarly migration current flux is the result of potential gradient described as

                                           (2.32)

As will be discussed in the spatial pattern formation section, migration current parallel to the electrode surface plays an important role in long range communication.

 

1.1.1.4  Mixed potential theory

 

The full consideration of the electrochemical cell during metal electrodissolution requires simultaneous consideration of anodic and cathodic kinetics taking place in the cell. Figure 10 represents such a diagram for nickel electrode immersed in an acid electrolyte. The simple straight lines for hydrogen and nickel redox reactions are based on Tafel equations for charge transfer polarization, and the polarization diagram is known as an Evans diagram. As can be seen, since the exchange currents for each reaction is at a different potential, the reaction current for each must evolve along the anodic or cathodic curve such that equilibrium potential can be reached. As can be seen in Figure 10 at this potential, also know as the corrosion potential, a corrosion current will be established causing the spontaneous dissolution of nickel electrode. The dissolution rate can be promoted along the anodic branch of the nickel curve with application of an overpotential. The polarization curves in Figure 6 and Figure 7 for example are as the result of an anodic overpotential in such a system.

Figure 10 schematics of electrochemical dissolution

 

The effect of build up of a concentration gradient at the electrode surface as the rate of reaction increases is illustrated with Stern deviations from the straight Tafel lines. With increasing potential, the reaction rate becomes completely controlled by mass transfer rate (ilim in Figure 10), which as demonstrated in the previous section is independent of the steady potential.

 

 

1.         Frank, U., Chemical oscillations. Angewandte chemie-international edition in english, 1978. 17(1): p. 1-15.

2.         Ertl, G., Oscillatory Kinetics and Spatiotemporal Self-Organization in Reactions at Solid-Surfaces. Science, 1991. 254(5039): p. 1750-1755.

3.         Hudson, J.L. and M.R. Bassett, Oscillatory Electrodissolution of Metals. Reviews in Chemical Engineering, 1991. 7(2): p. 109-170.

4.         Krischer, K., M. Eiswirth, and G. Ertl, Bifurcation-Analysis of an Oscillating Surface-Reaction Model. Surface Science, 1991. 251: p. 900-904.

5.         Wolf, W., et al., Experimental and theoretical description of potentiostatic current oscillations during H-2 oxidation. Journal of Electroanalytical Chemistry, 1995. 399(1-2): p. 185-196.

6.         Flatgen, G. and K. Krischer, Accelerating Fronts in an Electrochemical System Due to Global Coupling. Physical Review E, 1995. 51(5): p. 3997-4004.

7.         Sayer, J.C. and J.L. Hudson, Spatiotemporal Patterns on a Ring Electrode. Industrial & Engineering Chemistry Research, 1995. 34(10): p. 3246-3251.

8.         Dolata, M. and A.L. Kawczynski, Experimental investigations of chaotic and periodic oscillations during anodic dissolution of copper on rotating disc electrode. Polish Journal of Chemistry, 1999. 73(3): p. 519-526.

9.         Turing, A.M., The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences, 1952. 237(641): p. 37-72.

10.       Krischer, K. and A. Mikhailov, Bifurcation to Traveling Spots in Reaction-Diffusion Systems. Physical Review Letters, 1994. 73(23): p. 3165-3168.

11.       Nicolis, G., Introduction to nonlinear science. 1995, Cambridge ; New York: Cambridge University Press. xv, 254 p.

12.       Haim, D., et al., Modeling spatiotemporal patterns in anodic nickel dissolution. Chemical Engineering Science, 1992. 47(15-16): p. 3907-13.

13.       Russell, P. and J. Newman, Current Oscillations Observed within the Limiting Current Plateau for Iron in Sulfuric-Acid. Journal of the Electrochemical Society, 1986. 133(10): p. 2093-2097.

14.       Russell, P. and J. Newman, Anodic-Dissolution of Iron in Acidic Sulfate Electrolytes .1. Formation and Growth of a Porous Salt Film. Journal of the Electrochemical Society, 1986. 133(1): p. 59-69.

15.       Franck, U.F. and R. Fitzhugh, Periodische Elektrodenprozesse Und Ihre Beschreibung Durch Ein Mathematisches Modell. Zeitschrift Fur Elektrochemie, 1961. 65(2): p. 156-168.

16.       Mazouz, N. and K. Krischer, A theoretical study on turing patterns in electrochemical systems. Journal of Physical Chemistry B, 2000. 104(25): p. 6081-6090.

17.       Mazouz, N., G. Flatgen, and K. Krischer, Tuning the range of spatial coupling in electrochemical systems: From local via nonlocal to global coupling. Physical Review E, 1997. 55(3): p. 2260-2266.

18.       Levart, E. and Schuhman.D, Migration-Diffusion Coupling and Concept of Electrochemical Impedance. Journal of Electroanalytical Chemistry, 1970. 24(1): p. 41-&.

19.       Krischer, K., N. Mazouz, and G. Flatgen, Pattern formation in globally coupled electrochemical systems with an S-Shaped current-potential curve. Journal of Physical Chemistry B, 2000. 104(31): p. 7545-7553.

20.       Bertram, M. and A.S. Mikhailov, Pattern formation in a surface chemical reaction with global delayed feedback. Physical Review E, 2001. 6306(6): p. art. no.-066102.

21.       Zhai, Y.M., I.Z. Kiss, and J.L. Hudson, Emerging coherence of oscillating chemical reactions on arrays: Experiments and simulations. Industrial & Engineering Chemistry Research, 2004. 43(2): p. 315-326.

22.       Kiss, I.Z., W. Wang, and J.L. Hudson, Experiments on arrays of globally coupled periodic electrochemical oscillators. Journal of Physical Chemistry B, 1999. 103(51): p. 11433-11444.