Sample Space and Events

Example 1| Example 2 | Example 3 | Useful Web Resources | Solutions

.

Definition 1.1-1: Sample Space

A set of all possible outcomes of an experiment. The sample points are the elements in a sample space.

Example 1:

Consider a experiment that involves drawing 2 balls, one after the other, from a box that contains a blue ball, red ball and green ball. After a ball is drawn, it is replaced. So the sample space is S={BB,BR,BG,RB,RR,RG,GB,GR,GG}

What would the sample space in Example 1 be if the balls were not replaced?

      1. S={BR,BG,BB,RB,RG,GR,GB}
      2. S={BR,BG,BB,BR,RG,GR,GB}
      3. S={BR,BG,RB,RG,GR,GB}

    Solution

.

Definition 1.1-2:Event

An event is a subset of the sample space.

Example 2:

Consider tossing a fair coin three times. Let A be the event of getting at least one tail. What is A?

      1. A={HHT,HTH,THH,THT,TTH,HTT}
      2. A={HHT,HTH,THH,THT,TTH,HTT,TTT}
      3. A={HHT,HTH,THH}

    Solution

 

Definition 1.1-3: Mutually Exclusive

Two events A and B are mutually exclusive if they have no sample points in common, that is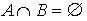

.

Example 3:

Which of the follwing are mutually exclusive events?

    1. A is the event of rolling a 5 on a fair dice, B is the event of rolling a 3 on a fair dice

    2. A is the event of rolling a 5 on a fair dice, B is the event of rolling an odd number on a fair dice

    3. A is the event of picking a Queen from a deck of playing cards, B is the event of picking a Heart from a deck of playing cards

    Solution

    .

Useful Web Resources

Sample Space and Events

Events and Random Variables

Chapter 2: Probability, Sample Space and Events-http://www.ece.concordia.ca/~gohari/engr371/2.pdf

Sample Space and Probability

    Solutions

Solution to Example 1

If you do not replace a ball after drawing it, you can never obtain a sample with two balls of the same colour. Both A) and B) are incorrect because the sample space contain a sample where the two balls have the same colour.

Solution to Example 2

"At least one tail" means that you could have one tail, two tails or three tails in the sample. So B) is correct because it contains all samples that contain one tail, two tails or three tails

Solution to Example 3

A) A is correct because you cannot roll a 5 and a 3 at the same time on a dice.

B) A and B are not mutually exclusive because rolling a 5 is common to both sets.

C) A and B are not mutually exclusive because picking the Queen of hearts is common to both sets.

 

Created by Ranodya Upathilake © Copyright 2002-2003. All rights reserved. Free Web Site Templates by JimWorld.com Designed by Finerdesign.com | Comments or Questions?