Assignment of Probabilities

Example 2| Example 5|Example 1.2-9| Useful Web Resources| Solutions

The General Mathematical Model:

P(A) = Number of points in A / Number of points in S

 

Example 1:

Let A be the event of drawing an Ace from a deck of 52 cards. What is P(A)?

Solution:

The sample space contains 52 points, because there are 52 cards in the deck. The event A contains 4 points because there are 4 aces in the deck. Therefore P(A)=4/52.

 

Example 2:

A box contains 3 blue balls, 6 white balls, and 2 red balls. What is the probability of picking a red ball? Type your solution in the space provided below and press ENTER.

Probability Axioms:

Now lets see how each of the axioms hold.

Let A be the event of getting tails when you flip a fair coin.

• Axiom 1: P(A)=1/2. Since P(A) is between 0 and 1, Axiom 1 holds.
• Axiom 2: S={Head,Tail}. P(S)=1/2 + 1/2= 1. So Axiom 2 holds.
• Axiom 3: Flipping a head and flipping a tail are two mutually exclusive events. Then P({Head} U {Tail}) = P({Head})+P({Tail})= 1/2 + 1/2 =1. So Axiom 3 holds.

Let A be the event of rolling a 2 on a dice.

• Axiom 1: P(A)=1/6=. Since P(A) is between 0 and 1, Axiom 1 holds.
• Axiom 2: S={1,2,3,4,5,6} P(S)=1/6 +1/6 + 1/6 + 1/6 +1/6 + 1/6=1.So Axiom 2 holds.
• Axiom 3: Rolling a 1,2,or5 are mutually exclusive events. Then P=({1} U {2} U {5}} =P({1}) + P({2}) + P({5}) =1/6 + 1/6 + 1/6= 1/2. So Axiom 3 holds.

Let A be the event of picking a king from a deck of cards.

• Axiom 1: P(A)= 4/52. Since P(A) is between 0 and 1, Axiom 1 holds.
• Axiom 2: S={AceHearts, AceDiamonds, AceClubs, AceSpades...., KingHearts, KingDiamonds, KingClubs, KingSpades) . P(S)=(1/52 + 1/52 + 1/52 +...+1/52)=1. Therefore Axiom 2 holds.
• Axiom 3: Picking a king from a deck of cards is mutally exclusive from picking a queen from the deck. So P({King}U{Queen})=P({King})+ P({Queen})= 4/52 + 4/52 = 8/52. So Axiom 3 holds.

Probability Law 1:

 

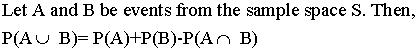
Example 4:

We want to find the probability of drawing an Ace or a Heart in a single draw from a deck of 52 cards.

Solution:

Let A be the event of drawing a King. Let B be the event of drawing a Heart. The P(A) is 4/52 because there are 4 Kings in a deck. The P(B)=13/52 because there are 13 Hearts in a deck. The interception of A and B is 1/52, because the deck contains one King of Hearts. So P(AUB)= 4/52 + 13/52 - 1/52= 16/52.

Probability Law 2:

 

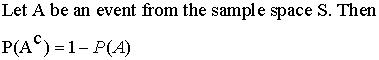
Example 5:

What is the probability of not drawing an Ace or a Heart in a single draw from a deck of 52 cards?

 

Excercise 1.2-9:

In a television game show, contestants are asked to match baby pictures of three celebrities with their respective adult pictures. Suppose a contestant matches the pictures at random.

A) What is the probability that all the pictures match?

B) What is the probability that none of the pictures match?