|
Example 1| Example 2 | Exercise 2.7-6 | Theorem 2.7-4 |Useful Web Resources| Solutions
Theorem 2.7-1:
Let X and Y have joint probability mass function p(x,y). Let W=Q(X,Y). Then,
Example 1:
Let X and Y have joint probability mass function.
x |
y |
p(x,y) |
0 |
1 |
2 |
| 1 |
0.15 |
0.10 |
0.25 |
| 2 |
0.35 |
0.10 |
0.05 |
Let W=(X^2)Y
E(W)= (1)^2(1)(0.10) + (2^2)(1)(0.25) +
(1^2)(2)(0.10) + (2^2)(2)(0.05) =
Let W=X(Y^2). What is E(W)?
Solution 
Theorem 2.7-2:
Let W=aX+bY. Then
E(W)=aE(X)+bE(Y)
Example 2:
Refer to Example 1 from above. Fill in the probability mass functions of X and Y below.
Please round all answers to one decimal place.
Solution
Free JavaScripts provided by The JavaScript Source
Theorem 2.7-3:
Let W= a1X1 +a2X2+ ... + anXn . Then
E(W)= a1E(X1) +a2E(X2)+ ... + anE(Xn)
Exercise 2.7-6:
The number of times a certain computer system crashes in a week is a random variable with probability mass function:
| y |
0 |
1 |
2 |
3 |
| p(y) |
0.5 |
0.3 |
0.15 |
0.05 |
Assume the number of crashes from week to week are independent.
D: What is the mean of the number of crashes in a year's time?
Solution
Theorem 2.7-4:
If X and Y are independent random variables, then
E(XY) = E(X)E(Y)
Are random variables X and Y from Example 1 independent?
Solution
Theorem 2.7-5:
Let W=aX+bY, where X and Y are independent random variables. Then,
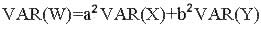
Theorem 2.7-6:
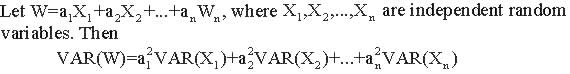
Theorem 2.7-7:
Let the random variables X1,X2,...,Xn be a random sample with E(Xi)= u and VAR(Xi)= s ^2, for i=1,2,...,n. Then
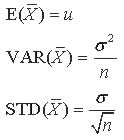
Theorem 2.7-8: Weak Law of Large Numbers
The notion that Xbar gets close to u as the size of the sample increases is the essence of the Law of Large Numbers. The following is the Weak Law of Large Numbers:
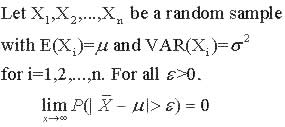
 Explore the law of large numbers by using the following applet!
Useful Web Resources
Jointly Distributed Random Variables
Jointly Distributed Variables -irving.vassar.edu/faculty/wl/Econ210/joint_prob.pdf
Solutions
Solution to Example 1
If W=(X^2)Y, then E(W)= (1)^2(1)(0.10) + (2^2)(1)(0.25) +(1^2)(2)(0.10) + (2^2)(2)(0.05) =0.1+1+0.2+0.4= 1.7
If W=X(Y^2) then E(W)=(1^2)(1)(0.1)+(1^2)(2)(0.25)+(2^2)(1)(0.1)+(2^2)(2)(0.05)=0.1+0.5+0.4+0.4= 1.4
Solution to Example 2
| x |
0 |
1 |
2 |
| p(x) |
0.15+0.35=0.5 |
0.1+0.1=0.2 |
0.25+0.05=0.30 |
| y |
1 |
2 |
| p(y) |
0.15+0.10+0.25=0.5 |
0.35+0.10+0.05=0.5 |
E(X)=0(0.5)+1(0.2)+2(0.3)=0.8
E(Y)=0(0.5)+1(0.5)=0.5
If W=6X-2Y, E(W)=E(6X-2Y)=6E(X)-2E(Y)=6(0.8)-2(0.5)=4.2-1=3.2
If W=11X+7Y+12, then E(W)=11E(X)+7E(Y)+12=11(0.8)+7(0.5)+12= 8.8 +3.5 +12 =24.3
If W=(X+7Y)/2, then E(W)=[E(X)+7E(Y)]/2= [0.8+7(0.5)] /2= 2.15
Solution to Exercise 2.7-6
A: E(Y)= 0(0.5)+1(0.3)+2(0.15)+3(0.05)=0.3+0.3+0.15=0.75
B: VAR(Y)= (0-0.75)^2(0.5) + (1-0.75)^2(0.3) + (2-0.75)^2(0.15) + (3-0.75)^2(0.05) =0.28125 + 0.01875 + 0.234375 + 0.253125 = 0.7875 = 0.79
C: Y represents the number of computer system crashes in a week. We want the TOTAL number of computer system crashes in a year. This can be expressed by the random variable W, where W=ΣYi where we take the sum of the Yi's for i=1, 2,...,52. Each Yi has the same probability distribution as the random variable Y. Since the number of crashes from week to week are independent, E(W) = ΣE(Yi) for i=1,2,...,52. Since the number of computer system crashes are independent from week to week, ΣE(Yi) = ΣE(Y)= E(Y)+E(Y)+...+E(Y). We add E(Y) 52 times. So our final aswer is
E(W) = Σ E(Yi) = Σ E(Y)= E(Y)+E(Y)+...+E(Y)= (52)(0.75)= 39 for i=1,2,...,52
D: Similarly, VAR(W)= ΣVAR(Yi) = ΣVAR(Y)= VAR(Y)+VAR(Y)+...+VAR(Y)= 52(0.79)= 41.08 for i=1,2,...,52
Solution to Theorem 2.7-4
E(XY)=(1)(1)(0.1)+(1)(2)(0.25)+(2)(1)(0.1)+(2)(2)(0.05)=0.9, and
E(X)E(Y)=(0.8)(0.5)= 0.4
So E(XY) does not equal E(X)E(Y). Therefore, X and Y are not independent.
.
.
|
