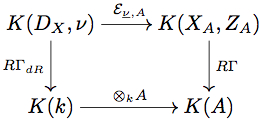
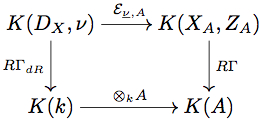
|
|
| Email: |
|
| De Rham epsilon factors for flat connections on higher local fields | Higher de Rham epsilon factors |
On the normally ordered tensor product and duality for Tate objects (joint with Braunling, Wolfson and Heleodoro) |
Cohomologically rigid local systems and integrality (joint with Esnault) |
Rigid connections and F-isocrystals (joint with Esnault) |
Mirror symmetry for moduli spaces of Higgs bundles via p-adic integration (joint with Wyss and Ziegler) |
