Hard plane wave source imposed along the line 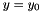 parallel to the z axis.
More...
parallel to the z axis.
More...
#include <HardPlaneWaveSource.hpp>
Public Member Functions | |
| HardPlaneWaveSource () | |
| HardPlaneWaveSource (const double incident_angle, const double y_coord, const double z_coord, const double freq, const double t_spread, const double s_spread) | |
| Create a plane wave source. | |
| HardPlaneWaveSource (const double incident_angle, const double y_coord, const double z_coord, const double freq, const unsigned nPeriods, const double s_spread) | |
| Create a plane wave source. | |
| HardPlaneWaveSource (const double incident_angle, const double y_coord, const double freq, const double t_spread) | |
| Create a plane wave source. | |
| double | getSpatialWaveform (const double z) const |
Calculate the spatial waveform 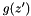 , where. , where. | |
| double | getTemporalWaveform (const double t, const double z, const double v_p) const |
Calculate the temporal waveform 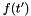 , where. , where. | |
| double | getFrequency () |
Public Attributes | |
| double | theta |
| double | y_0 |
| double | z_0 |
| Function * | f_t |
Temporal waveform, 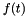 . . | |
| Function * | g_z |
Spatial waveform, 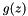 . . | |
| double | T |
| Time span of the source. | |
Detailed Description
Hard plane wave source imposed along the line 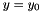 parallel to the z axis.
parallel to the z axis.
The acoustic pressure imposed along the this line is given by
![\[ p(z, t) = f(t') g(z') \]](form_91.png)
where 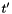 and
and 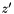 denote the transform variables as functions of the real variables
denote the transform variables as functions of the real variables 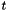 and
and 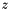 ,
, 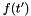 denotes the temporal waveform and
denotes the temporal waveform and 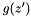 denotes the spatial waveform,
denotes the spatial waveform,
Constructor & Destructor Documentation
| HardPlaneWaveSource::HardPlaneWaveSource | ( | ) |
| HardPlaneWaveSource::HardPlaneWaveSource | ( | const double | incident_angle, |
| const double | y_coord, | ||
| const double | z_coord, | ||
| const double | freq, | ||
| const double | t_spread, | ||
| const double | s_spread | ||
| ) |
Create a plane wave source.
The temporal shape 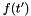 is a GaussianModulatedSinusoid waveform with the carrier frequency being
is a GaussianModulatedSinusoid waveform with the carrier frequency being 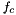 , the standard deviation being
, the standard deviation being 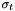 and the mean being
and the mean being 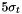 . The spatial shape
. The spatial shape 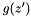 is a Gaussian waveform with the standard deviation being
is a Gaussian waveform with the standard deviation being 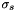 and the mean being 0.
and the mean being 0.
The time span of this plane wave source is 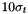 .
.
- Parameters
-
incident_angle (rad) incident angle 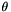
y_coord anchor position 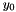
z_coord anchor position 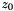
freq carrier frequency 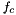
t_spread temporal standard deviation 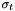
s_spread spatial standard deviation 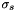
| HardPlaneWaveSource::HardPlaneWaveSource | ( | const double | incident_angle, |
| const double | y_coord, | ||
| const double | z_coord, | ||
| const double | freq, | ||
| const unsigned | nPeriods, | ||
| const double | s_spread | ||
| ) |
Create a plane wave source.
The temporal shape 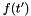 is a ramp modulated Sinusoid waveform with the carrier frequency being
is a ramp modulated Sinusoid waveform with the carrier frequency being 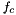 . The first temporal peak appears after 3 periods. The spatial shape
. The first temporal peak appears after 3 periods. The spatial shape 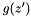 is a Gaussian waveform with the stardard deviation being
is a Gaussian waveform with the stardard deviation being 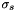 and the mean being 0.
and the mean being 0.
- Parameters
-
incident_angle (rad) incident angle 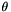
y_coord anchor position 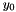
z_coord anchor position 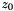
freq carrier frequency 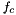
nPeriods number of periods of the Sinusoid waveform s_spread spatial spreading 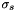
| HardPlaneWaveSource::HardPlaneWaveSource | ( | const double | incident_angle, |
| const double | y_coord, | ||
| const double | freq, | ||
| const double | t_spread | ||
| ) |
Create a plane wave source.
The temporal shape 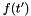 is a GaussianModulatedSinusoid waveform with the carrier frequency being
is a GaussianModulatedSinusoid waveform with the carrier frequency being 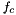 , the standard deviation being
, the standard deviation being 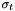 , and the mean being
, and the mean being 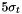 . The spatial shape is a constant.
. The spatial shape is a constant.
The time span of this plane wave source is 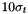 .
.
- Parameters
-
incident_angle (rad) incident angle 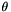
y_coord anchor position 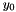
freq carrier frequency 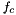
t_spread temporal standard deviation 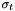
Member Function Documentation
| double HardPlaneWaveSource::getFrequency | ( | ) |
| double HardPlaneWaveSource::getSpatialWaveform | ( | const double | z | ) | const |
Calculate the spatial waveform 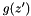 , where.
, where.
![\[ z{'} = (z-z_0)\cos(\frac{\pi}{2}-\theta) \]](form_108.png)
| double HardPlaneWaveSource::getTemporalWaveform | ( | const double | t, |
| const double | z, | ||
| const double | v_p | ||
| ) | const |
Calculate the temporal waveform 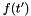 , where.
, where.
![\[ t' = t-\frac{(z-z_0)\sin(\frac{\pi}{2}-\theta)}{v_p}, 0\le t \le T \]](form_109.png)
Member Data Documentation
| Function* HardPlaneWaveSource::f_t |
Temporal waveform, 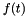 .
.
| Function* HardPlaneWaveSource::g_z |
Spatial waveform, 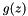 .
.
| double HardPlaneWaveSource::T |
Time span of the source.
| double HardPlaneWaveSource::theta |
| double HardPlaneWaveSource::y_0 |
| double HardPlaneWaveSource::z_0 |
The documentation for this class was generated from the following files:
- include/HardPlaneWaveSource.hpp
- src/HardPlaneWaveSource.cpp
 1.8.1.2
1.8.1.2