





Nächste Seite: Der zufällige Meßfehler
Aufwärts: Statistik
Vorherige Seite: Statistik
Inhalt
Index
In meiner Arbeit werden für Regressionsrechnungen die folgenden, nach
Algorithmen aus Noack (1980) berechneten statistischen Kennwerte
benutzt:
- Die Varianz der Residuen. Sie berechnet sich aus der Summe
der Abweichungsquadrate zwischen Meßpunkt und errechneter Kurve
(d.h. der Regressionsgeraden), geteilt durch die Anzahl der
Meßpunkte minus 1.
- Die Standardabweichung der Residuen. Sie errechnet sich aus
der Quadratwurzel der oben beschriebenen Varianz.
- Der Betrag des Korrelationskoeffizienten: Zunächst wird zur
Berechnung das Verhältnis der Varianz der Residuen zur Varianz aller
Datenpaare gebildet. Der Korrelationskoeffizient errechnet sich aus
der Quadratwurzel dieses Verhältnisses. Der Korrelationskoeffizient
kann Werte zwischen 0 und 1 annehmen. Je größer der Wert, desto
besser wird der Zusammenhang der Meßwerte durch die errechnete Kurve
beschrieben. Ein Wert von 1 etwa bedeutet, daß alle Datenpaare auf
der Kurve liegen. Ein Wert von 0 bedeutet, daß die berechnete Kurve
überhaupt keinen Zusammenhang mit den Datenpaaren hat. Man beachte
jedoch: Der Korrelationskoeffizient ist ein absolutes Maß und läßt
alleine keinen Rückschluß auf einen tatsächlichen Zusammenhang
zwischen den Daten und der Kurve zu. Er muß immer im Zusammenhang
mit der Anzahl der Meßwerte interpretiert werden!
- Die Anzahl der Freiheitsgrade dF errechnet sich aus: Anzahl
der Daten-Paare minus Anzahl der geschätzten Parameter. Ein
Beispiel: Die Anzahl der gültigen Daten-Paare sei 30. Bei einer
Polynom-Regression 2. Grades ist dann
df = 30 - 3 = 27.
- Die Irrtumswahrscheinlichkeit p. p = 1 bedeutet hier eine
Irrtumswahrscheinlichkeit von 100%, analog dazu bedeutet
p
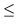 0.05 eine Irrtumswahrscheinlichkeit von kleiner oder gleich 5%.
Ein Wert
p
0.05 eine Irrtumswahrscheinlichkeit von kleiner oder gleich 5%.
Ein Wert
p 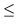 0.01 bedeutet z.B., daß der gefundene
Korrelationskoeffizient mit höchstens 1% Unsicherheit keinen
zufälligen Zusammenhang zwischen Datenpaaren und errechneter Kurve
beschreibt.
0.01 bedeutet z.B., daß der gefundene
Korrelationskoeffizient mit höchstens 1% Unsicherheit keinen
zufälligen Zusammenhang zwischen Datenpaaren und errechneter Kurve
beschreibt.
- Die Determinationskoeffizienten Eta2 und
Eta2adj (im
Text auch häufig als r2 bezeichnet). Der Koeffizient Eta2 ist
das Quadrat des Korrelationskoeffizienten und gibt den Anteil der
Varianz an, der durch die Regression aufgeklärt wird. Zusätzlich
wird mit
Eta2adj ein weiterer Koeffizient ausgegeben, der eine
bessere Schätzung der aufgeklärten Varianz liefert. Die Berechnung
erfolgt nach der Formel
Eta2adj = 1 - 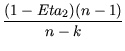
|
(2.2) |
Hierbei ist: Eta2 = Varianz der Residuen beziehungsweise die
Varianz aller Datenpaare, n = Anzahl der Meßwert-Paare, k = Anzahl
der geschätzten Parameter.






Nächste Seite: Der zufällige Meßfehler
Aufwärts: Statistik
Vorherige Seite: Statistik
Inhalt
Index
Wortmann U.G., (1996). Zur Ursache der hemipelagischen....
Last updated by Uli Wortmann 1999-03-09