





Nächste Seite: Der systematische Meßfehler
Aufwärts: Statistik
Vorherige Seite: Statistische Kennwerte bei Regressionsrechnungen
Inhalt
Index
Unterabschnitte
Unter dem zufälligen Meßfehler wird die
Abweichung einer Einzelmessung vom Durchschnitt einer großen Anzahl
gleichartiger Messungen verstanden. Zur Bestimmung desselben wurden
aus einer Probe zehn unabhängig voneinander aufbereitete und
analysierte Proben hergestellt, so daß hiermit zufällige Variationen,
die durch die Aufbereitungs- und Meßtechnik bedingt sind, erfaßt
werden. Eine Übersicht der so ermittelten Fehlerwerte gibt
Tabelle2.2.
Zusätzlich wurde untersucht, inwieweit sich der
Verwitterungszustand des Gesteins auf die Meßwerte auswirkt. Um
den Einfluß der Verwitterung abzuschätzen, wurde versucht, den
größtmöglichen Verwitterungseffekt zu erfassen. Hierzu wurde,
ausgehend von der Probennahmestelle im kompakten Gestein, ein
Marker-Horizont in immer stärker verwitterte Bereiche verfolgt und
beprobt (Abb.2.7). Die damit ermittelte Variation des
Signals wurde in die Fehlerrechnung aufgenommen. Der so ermittelte
Fehler ist für die meisten Elemente etwa doppelt so groß wie die reine
Meßungenauigkeit. Da dieser Wert zu realistischeren Abschätzungen
der Genauigkeit der Daten führt, wird er in dieser Arbeit prinzipiell
als Substitut für den zufälligen Meßfehler verwendet. Tabelle
2.3 zeigt eine Aufstellung der nach diesem Verfahren
ermittelten Fehlergrenzen.
Die sich hieraus ergebenden Toleranzbreiten sind in den
Diagrammen nur dann angegeben, wenn sie eine für das gemessene Signal
bedeutsame Größenordnung erreichen, ansonsten werden sie grundsätzlich
weggelassen.
Die mit der klassischen Fehlerrechnung erzielten Resultate beziehen
sich auf ein Signifikanzniveau von 68.26% (Schönwiese, 1992) und sind
somit nicht sonderlich aussagekräftig. Die in meiner Arbeit
angegebenen Meßfehler (Tab.2.3) beziehen sich
grundsätzlich auf ein Signifikanzniveau von 95%. Die Berechnung auf
dem Signifikanzniveau von 95% erfolgt dabei nach folgendem
Verfahren:
Hierbei ist s die Standardabweichung und z ein Skalierungsfaktor,
der abhängig von Stichprobenumfang und Signifikanzniveau ist und
einschlägigen Tabellen entnommen werden kann (z.B. Schönwiese, 1992).
Da in dieser Arbeit hauptsächlich Element-Verhältnisse betrachtet
werden, muß bei der Fehlerrechnung noch die Fehlerübertragung
durch die Normierung auf Aluminium berücksichtigt werden. Nach
Schönwiese (1992) hat der aus den Größen a und b gebildete
Quotient E einen relativen Gesamtfehler  E, der sich aus
den relativen Einzelfehlern
E, der sich aus
den relativen Einzelfehlern  a und
a und  b
folgendermaßen berechnet:
Der absolute Gesamtfehler
b
folgendermaßen berechnet:
Der absolute Gesamtfehler 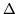 E ergibt sich aus dem relativen
Fehler
E ergibt sich aus dem relativen
Fehler  E und dem arithmetischen Mittel der Meßwerte
E und dem arithmetischen Mittel der Meßwerte 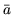 und
und 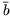 als
als






Nächste Seite: Der systematische Meßfehler
Aufwärts: Statistik
Vorherige Seite: Statistische Kennwerte bei Regressionsrechnungen
Inhalt
Index
Wortmann U.G., (1996). Zur Ursache der hemipelagischen....
Last updated by Uli Wortmann 1999-03-09