
|
|
Research
|
| |
- Financial engineering, optimal control, high-performance computing
- Numerical methods for partial integro-differential equations, arising in option pricing with jump-diffusion and Levy processes
- Stochastic optimal control and Hamilton-Jacobi-Bellman equations, arising in pricing in incomplete markets
- Application of high-performance architectures, such as Cell BE or GPU, to solve aforementioned problems quickly
- Efficient Construction of Robust Hedging Strategies under Jump Models (with Matt Davison) (March 3, 2010) [SSRN] [BIB]
Markets where asset prices follow processes with jumps are incomplete and any portfolio hedging against large movements in the price of the underlying asset must include other instruments. The standard approach in literature is to minimize the price variance of the hedging portfolio under a certain choice for the jump size distribution. This paper generalizes the hedging strategy of Kennedy, Forsyth, and Vetzal (2009) to minimize the weighted variance of hedging portfolio price and Greeks (sensitivities of portfolio values to changes in the state variables or models parameters). The new approach yields improved hedging portfolios over long horizons (i.e. semi-static and static hedging) and for non-stationary model parameters (e.g. stochastic volatility or jump arrival rate). From the computational perspective, this paper develops a new Fourier transform-based numerical method for computing the Greeks of European options with arbitrary payoffs by extending the work of Jackson, Jaimungal, and Surkov (2008). The new computational method allows to rapidly compute the hedging portfolio weights of the generalized hedging approach. We demonstrate the precision and efficiency of the new numerical scheme and perform a comparative analysis of various hedging approaches.
- Valuing Early Exercise Interest Rate Options with Multi-Factor Affine Models (with Sebastian Jaimungal) (March 3, 2010) [SSRN] [BIB]
Multi-factor interest rate models are widely used in practice. Quite often, contingent claims with earlier exercise features are valued by resorting to trees, finite-difference schemes and Monte Carlo simulations. However, when jumps are present these methods are less accurate and/or efficient. In this work we develop an algorithm based on a sequence of measure changes coupled with Fourier transform solutions of the pricing partial-integro differential equation to solve the pricing problem. The method, coined the irFST method, also neatly computes option sensitivities. Furthermore, we develop closed form formulae for accrual swaps and accrual range notes under our multi-factor jump-diffusion model. We demonstrate the versatility and precision of the method through numerical experiments on European, Bermudan and callable bond options, (accrual) swaps and range notes.
- Efficient Fourier Transform-based Pricing of Interest Rate Derivatives (March 10, 2009) [PDF]
Young Researchers Workshop on Finance 2010, Tokyo Metropolitan University
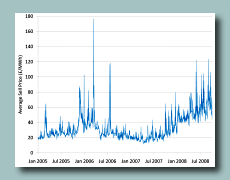
- Pricing and Hedging of Commodity Derivatives using FFT (December 9, 2009) [PDF]
Department of Mathematics and Statistics, University of Calgary
-
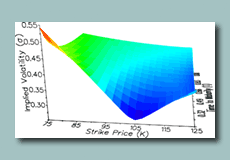
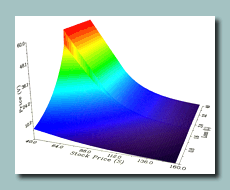
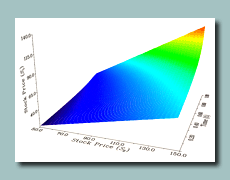
FST is a generic framework based on the Fourier transform for pricing and hedging of various options in equity, commodity, currency, and insurance markets. The FST framework circumvents the problems associated with the existing finite difference methods by utilizing the Fourier transform to solve the PIDE, with resulting method being highly efficient and rapidly convergent. FST-based algorithms can can be applied to pricing of a wide range of options such as European, Bermudan, American, barrier, and other options. The dynamics of the stock price process can be modeled by any exponential Levy model, such as Black-Scholes-Merton, Merton jump-diffsuion, Kou jump-diffusion, Variance Gamma, Normal inverse Gaussian and CGMY models, with mean-reversion or regime-switching being easily handled.
- The raytracer was written from scratch in C++ for an undergraduate project in graphics. Some of the features implemented include: anti-aliasing, reflections, refractions, bounding volume hierarchies, bitmap and mathematical textures.
|
|
|









