Die Fourier-Transformation

Ohne in diesem Abschnitt auf die Details der Fourier-Transformation einzugehen, sollen kurz einige wichtige Begriffe erläutert werden. Eine gute Einführung in die Problemstellung findet sich in Bracewell (1989), eine umfangreiche Diskussion in Priestley (1981). Die in der vorliegenden Arbeit verwendeten Algorithmen und ihre Implementation sind ausführlich in Press et al. (1992) beschrieben.

1822 publizierte Jean-Baptiste-Joseph Fourier sein Buch ,,Die analytische Theorie der Wärme``. Hierin gelang es ihm zu zeigen, daß man eine unstetige, d.h. sprunghafte Funktion durch die Summe unendlich vieler Sinusfunktionen darstellen kann. Somit wurde es möglich, einen physikalischen Prozeß, den man anhand der zeitlichen Änderung einer Größe h(t) charakterisieren kann (z.B. der C_org-Gehalt in Abhängigkeit vom Alter), durch eine Summe von Sinusfunktionen, die durch ihre Amplituden H(f ) in Abhängigkeit von der Frequenz charakterisiert werden, zu beschreiben. h(t) und H(f ) sind also zwei verschiedene Repräsentationen der gleichen Funktion. Mit Hilfe der Fourier-Transformation kann man zwischen den beiden Darstellungen wechseln:

$$\int_{-\infty}^{\infty} \pi \int_{-\infty}^{\infty} \pi$$ (2.8)

Trägt man die Frequenzen auf der x-Achse und die zugehörigen Amplituden auf der y-Achse auf, erhält man ein Frequenzspektrum. Enthält die Funktion h(t) periodische Anteile, werden die Amplituden der Frequenzen, die die periodischen Anteile betreffen, größer sein als die Amplituden, welche die nicht-periodischen Anteile beschreiben.

Beim Übergang zu diskret gemessenen Daten werden die Zusammenhänge schwieriger. Mißt man eine Funktion h(t) in den Zeitabständen $\Delta$t, so gibt es eine spezielle Frequenz f_c, die sogenannte Nyquist-Frequenz

$${\frac{1}{2\Delta t}}$$ (2.9)

welche die Obergrenze der durch die Fourier-Transformation noch erfaßbaren Frequenzen darstellt. Transformiert man ein Signal, das Frequenzen oberhalb der Nyquist-Frequenz enthält, werden diese auf die Frequenzen unterhalb der Nyquist-Frequenz abgebildet. Sie erzeugen dabei sogenannte Spiegelfrequenzen (aliasing), die das eigentliche Signal verfälschen. Im Falle der vorliegenden Arbeit heißt das, daß bei einer Beprobungsrate von 3 cm bestenfalls Periodenlängen von etwa 6 cm aufgelöst werden können. Außerdem ist damit zu rechnen, daß aufgrund der Spiegelfrequenzen die Frequenzen unterhalb der Nyquist-Frequenz verfälscht werden.

Zur Fourier-Transformation wird ein leicht modifizierter Algorithmus der sogenannten ,,Fast Fourier-Transformation`` (FFT) aus Press et al. (1992) benutzt. Das Programm ist so modifiziert worden, daß das resultierende ,,Frequenz-Spektrum``, unabhängig von der Beprobungsrate $\Delta$ und der Profillänge, in das Intervall zwischen 0 und 1 abgebildet wird. Das heißt, ein Signal das nur aus einer Frequenz besteht, hätte im zugehörigen Frequenz-Spektrum den Amplitudenwert eins. Die Transformation ist außerdem so gewählt, daß wenn das zu untersuchende Signal aus zwei Frequenzen bestände von denen die eine doppelt so stark ist wie die andere, die Amplituden im Frequenzspektrum H(f ) sich ebenfalls wie eins zu zwei verhalten. Um die Lesbarkeit der Analysen zu erhöhen, wurden die Amplituden H(f ) in Abhängigkeit von der Periodenlänge (d.h. H($\lambda$)) ausgedrückt, so daß in den Diagrammen direkt die Periodenlänge in Zentimetern abgelesen werden kann.

Um die Signifikanz der FFT-Ergebnisse zu beurteilen, werden häufig Vertrauensintervalle angegeben. Da natürliche Ereignisse, wie zum Beispiel Erdbeben, Abflußschwankungen oder Niederschlagsmengen, in der Regel quasi-periodische Prozesse darstellen (Mandelbrot, 1983), liefert die Analyse solcher Prozesse in jedem Fall signifikante Frequenzen. Aus diesem Grund verzichte ich auf die Angabe von Vertrauensintervallen.

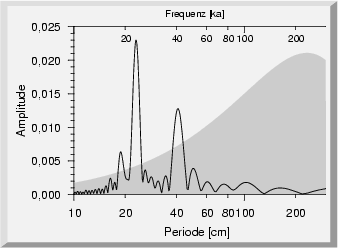
Stattdessen soll das Ergebnis mit dem Spektrum eines ,,natürlichen`` quasi-periodischen Prozesses verglichen werden, dem sogenannten ,,roten Rauschen`` (Voss & Clarke, 1975; Voss, 1982). Die Chaosforschung ermöglicht die mathematische Modellierung solch quasi-periodischer, aber zufälliger Prozesse. Im vorliegenden Fall wird ein fraktales Rauschen (Voss & Clarke, 1975) der Dimension 0.2 und 0.5 benutzt (Abb.2.8).

Abbildung 2.8: Beispiel zur Darstellung der FFT-Analysen anhand der Daten von Berger & Loutre (1991) für das Quartär. Der grau schattierte Bereich stellt das hypothetische Spektrum eines quasi-periodischen, aber zufälligen Prozesses dar. Die in schwarz dargestellte FFT der Meßergebnisse wird nur dann als signifikant erachtet, wenn sie das graue Spektrum übersteigt. Die untere Skala zeigt die Periodenlängen so wie sie sich aus den Felddaten ergeben. Die obere Skala gibt die zugehörigen Frequenzen an. Für die Umrechnung wurde nicht die ursprünglich zu 9 mm/ka abgeschätzte Sedimentationsrate sondern der auf 7.5 mm/ka korrigierte Wert benutzt (s. auch Abschnitt5.4).

Die Erzeugung der Daten erfolgte nach einem Algorithmus aus Peitgen & Saupe (1988).

Ein weiterer kritischer Punkt bei der FFT-Analyse betrifft das Problem der Stationarität. Das bedeutet, daß sich das Zeitintervall zwischen den einzelnen Proben nicht ändern darf - ein bei geologischen Profilen nicht zu unterschätzendes Problem. Um das Kriterium der Stationarität erfüllen zu können, müssen die vorliegenden Daten zunächst in eine stationär beprobte Zeitreihe überführt werden. Es wird dabei implizit angenommen, daß sich die Zeitachse prinzipiell durch ein zehnfach feineres Muster beschreiben läßt. Die fehlenden Zwischenwerte werden dabei durch lineare Interpolation gewonnen. Die resultierende Meßreihe wird dann anschließend mit einem definierten Zeitschritt neu abgetastet. Da per Definition der Aluminiumgehalt ein Maß für die relative Sedimentationsgeschwindigkeit darstellen soll (siehe Abschnitt.2.3), wird die Abweichung vom Mittelwert zur Korrektur der Probenabstände benutzt:

$${\frac{\mathrm{Abstand}\times \mathrm{Al}}{\mathrm{\overline{Al}}}}$$ (2.10)

Diese Daten werden vor der Fourier-Transformation noch einer Mittelwertskorrektur unterworfen und in das Intervall [0,1] projiziert. Um unerwünschte, Analysen-bedingte Artefakte zu unterdrücken, wird die resultierende Meßreihe anschließend bis zur nächst größeren Potenz zur Basis 2, mit Nullen aufgefüllt (zero-padding; Press et al., 1992).

Um aus den bei der FFT erhaltenen Periodenlängen Frequenzen zu berechnen, muß die Sedimentationsrate bestimmt werden. Hierzu stehen die stratigraphischen Grenzen Tristel-Formation/Flysch-Gault (tiefes Apt) und Flysch-Gault/Reiselsberger Sandstein (unteres Cenoman) zur Verfügung (Pflaumann, 1964). Legt man die Zeitskala von Harland et al. (1990) zugrunde, so ergibt sich ein Zeitraum von rund 24 Mio.J. (s. Abb.1.4). Bei einer Mächtigkeit des Flysch-Gault von 220 m und unter der Annahme, daß das Erosionspotential der Trübeströme etwa der Mächtigkeit der abgelagerten Turbidite entspricht (s. Abschnitt3.4), ergibt sich eine Sedimentationsrate von etwa 9 mm/ka. Obwohl dieser Wert aufgrund des Fehlens einer Stufengliederung des Apts und Albs für den Flysch-Gault mit Unsicherheiten behaftet ist, entspricht er größenordnungsmäßig dem Wert aus ähnlichen, aber stratigraphisch besser gegliederten Becken, wie zum Beispiel dem Kap Verde-Becken (8 mm/ka im späten Apt; Dean et al., 1978).

Die so erhaltenen Frequenzen sind in den FFT-Diagrammen als zweite Skala mit angegeben (Abb.2.8). Da sich bei der späteren Auswertung der Daten gezeigt hat, daß sich bei Korrektur der Sedimentationsrate von 9 mm/ka auf 7.5 mm/ka eine gute Übereinstimmung der kretazischen Milankovic-Frequenzen (Berger & Loutre, 1989) mit den hier gemessenen Perioden ergibt, wurde für die Umrechnung der auf 7.5 mm/ka korrigierte Wert benutzt (s. auch Abschnitt5.4).